Problema 11 del concurso marató de problemes 2019
Se dirige a una edad de: 14-15 años

Marina tiene dibujado un triángulo isósceles.

Llamaremos base al lado de longitud diferente a los otros dos.

Desde uno de los vértices de la base, Marina traza un segmento hasta el lado opuesto, cuya longitud es igual a la longitud de la base.

Desde el punto obtenido, traza un segmento de la misma longitud que la base original que le lleva hasta el otro lado del triángulo original.

Desde ese otro punto, vuelve a trazar otro segmento hasta el otro lado del triángulo original que de nuevo tiene la misma longitud que la base.

En ese momento, se da cuenta de que la distancia desde el último punto hasta el vértice entre lados iguales del triángulo original, también es igual que la base, con lo que Marina ha descompuesto el triángulo original en cuatro triángulos que tienen dos lados, al menos, con la misma longitud que la base original.

¿Puedes dar la medida del ángulo opuesto a la base del triángulo original?

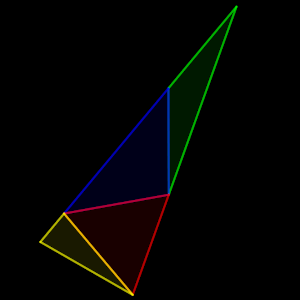
Solución:

En un triángulo isósceles, hay dos ángulos iguales y uno diferente. Si el triángulo isósceles tiene x como ángulo igual, resulta que el diferente debe medir 180º – 2x para que los tres sumen 180º.

Ahora, si llamamos a al ángulo desigual del triángulo original, por ejemplo, y b al ángulo repetido del segundo triángulo empezando a mirar desde este ángulo desigual, tenemos que, para que el segmento donde coinciden ambos sea recto, debe medir 180º = 180º – 2a + b, de forma que b = 2a.

Pero ahora, si llamamos c al ángulo repetido del tercer triángulo, tenemos que c + 180º – 2b + a = 180º, por lo que c + a = 2b = 4a, por lo que c = 3a.

También es cierto que, si llamamos d al ángulo repetido del cuarto triángulo, tenemos que d + 180º – 2c + b = 180º, por lo que d + b = 2c, por lo que d + 2a = 6a, y por tanto d = 4a.

Por último, mirando al triángulo al completo, vemos que 4a + 4a + a tienen que sumar 180º, y por tanto a = 20º.