Problema 2 del concurso Olitele 2020 Se dirige a una edad de: 16-17 años
El área sombreada de la figura siguiente mide a·π para cierto número entero a.
¿Cuál es el valor de a?
Por si no aprecias bien la figura, se trata de un cuarto de circunferencia dentro del cual se ha cortado una circunferencia tangente a uno de los radios que la limitan. El único dato es que la longitud del segmento tangente paralelo al radio al que es tangente la circunferencia interior mide, desde el radio que limita el cuarto de circunferencia hasta la propia circunferencia, 12 unidades. El dato del área se debe expresar, como es habitual, en unidades cuadradas.
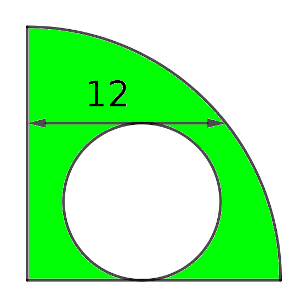
Solución:
La idea es relacionar el radio de ambas circunferencias y el valor 12, y calcular el área a partir de esa relación.
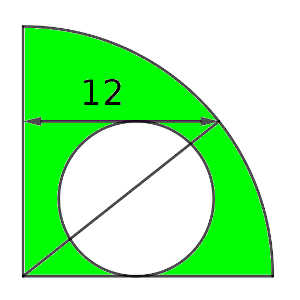
Para ello, llamaremos R al radio de la circunferencia grande, y r al de la pequeña, y trazaremos un radio que marque el punto de intersección entre la circunferencia exterior y la tangente interior a la interior, que es la única medida que tenemos.
Puesto que todos los radios miden lo mismo, tenemos que R² = (2r)² + 144, es decir, que R² = 4r² + 144. Esa es la relación entre ambos valores.
Puesto que el área de la figura es πR²/4 – πr² = π(R²/4 – 4r²/4) = π(R² – 4r²)/4 = π·144/4 = 36·π.
Es decir que el valor de a que se pide es 36.