Problema 1 de la Fase Local de la Olimpiada Española de Matemáticas 2021
Se dirige a una edad de: 16-17 años

Determinar todos los números de cuatro cifras abcd tales que al insertar un dígito 0 en cualquier posición se obtiene un múltiplo de 7.

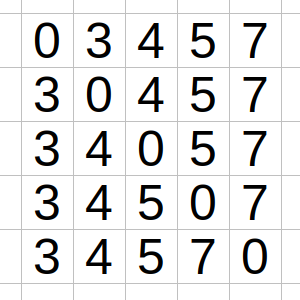
Solución:

Es una cuestión bastante sencilla, pero la clave para obtener todos los puntos está en explicarlo bien.

Observando lo que sucede en casos particulares, lo que debemos plantearnos es cómo son los diferentes números que obtenemos insertando una cifra cero (hay un detalle importante en que al leer “en cualquier posición” debemos pensar que el cero es posible insertarlo también en primera o última posición).

Para obtener información podemos tratar de “verlo” con los números de dos cifras, que hay pocos múltiplos de 7 entre ellos (es evidente que insertar un cero en la primera posición lo deja igual), estudiando qué les ocurre a los diferentes números.

Hay un ejemplo en el dibujo de un número de cuatro cifras al que se le ha insertado un número en las cinco posiciones posibles.

Ahora bien, si los números son múltiplos de 7, su diferencia también lo será, y en ella eliminaremos la mayor parte de las cifras.

En efecto, si restamos, por ejemplo, 30457 y 03457, obtenemos 27000, que evidentemente no es múltiplo de 7.

Algebraicamente el número abcd se puede expresar como 1000a + 100b + 10c + d. Entonces, la diferencia entre 10000a + 100b + 10c + d y 1000a + 100b + 10c + d es 9000a, y si debe ser múltiplo de 7, también lo debe ser a.

Eso se puede apreciar para cualquier cifra del número, por lo que todas ellas deben ser, bien 7 o bien 0. Excepto la primera, que debe ser diferente de cero para que el número sea considerado de cuatro cifras propiamente.

Por lo tanto, los números con esta propiedad serán 7000, 7007, 7070, 7077, 7700, 7707, 7770 y 7777, un total de 8 números.