Problema 2 de la Fase Local de la Olimpiada Española de Matemáticas 2021
Se dirige a una edad de: 16-17 años

Determinar todas las parejas de enteros positivos (m, n) para los cuales es posible colocar algunas piedras en las casillas de un tablero de m filas y n columnas, no más de una piedra por casilla, de manera que todas las columnas tengan la misma cantidad de piedras, y no existan dos filas con la misma cantidad de piedras.

Solución:

Evidentemente, si m = 1, n puede valer cualquier cantidad, ya que poniendo una piedra en cada casilla tendríamos una situación como la que buscamos.

Si m = 2, n también puede tener cualquier valor. Si n = 1, situaríamos una piedra en una de las casillas, si n = 2, deberíamos situar una piedra en las dos casillas de una misma fila, y para valores mayores de n, podríamos situar menos piedras en una de las filas que en otra, siempre una piedra por columna, para tener una situación como la pedida.

Veamos qué ocurre para m = 3. Está claro que n no puede valer 1, ya que no podemos conseguir en esas condiciones que las tres casillas sean diferentes. El caso n = 2 es más interesante, ya que en el caso de que las tres filas tengan cantidades diferentes de piedras, nos encontraremos con que tenemos todos los posibles valores entre 0 y 2, lo que supone un total de 0 + 1 + 2 = 3 piedras en total. Pero ese número es una cantidad impar, y no podríamos conseguir que las dos columnas tuviesen la misma cantidad de piedras. Por tanto, n no puede valer 2.

Sin embargo, n puede valer 3, como vemos en la imagen (1 – 2 – 3 piedras).

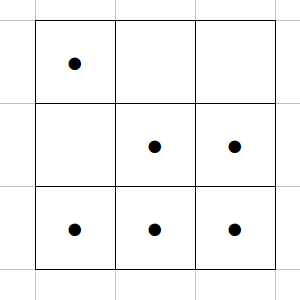
Y para crear tableros con n mayor, es suficiente añadir piedras sólo a las filas que tienen más, para que todas tengan cantidades diferentes. La cantidad de filas a la que habrá que añadir más es el número de piedras que hay en cada una de las columnas previas.

Una conclusión podemos sacar ya. En el momento en que un tablero de m filas se pueda llenar, tableros con más columnas es posible llenarlos siempre. Por lo tanto, para cada m, hay un tablero de un número mínimo de n columnas que se puede llenar en las condiciones del problema, todos los que tengan un valor de n superior se podrán llenar y todos los que tengan n inferior no podrán llenarse.

Antes de dar una idea más general, vamos a proseguir nuestra investigación, para tener más evidencias.

¿Que sucede para 4 filas? Es decir, si m vale 4.

Está claro que si n vale 2 no es posible, ya que si las 4 filas deben tener cantidades diferentes, debemos tener más posibilidades que 0 – 1 – 2. Pero resulta que para n = 3 sí lo es (como 0 + 1 + 2 + 3) = 6, al dividir resulta dar 2, así que podemos hacer el siguiente reparto:

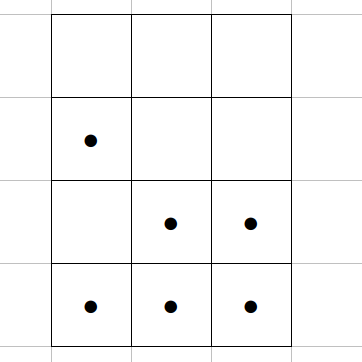
Por lo tanto, para m = 4 el valor de n mínimo es de 3, igual que para el valor de m = 3.

Continuando el proceso, para el valor de m = 5, se puede deducir que es imposible que n sea inferior a 4, porque no como mínimo debe haber 5 valores numéricos entre 0 y n, pero 4 también es imposible, ya que 0 + 1 + 2 + 3 + 4 = 10, y no es divisible entre n = 4.

El valor de n = 5 sí se puede rellenar, ya que 0 + 1 + 2 + 3 +4 = 10 sí es divisible por 5, y podemos situar las piedras de la siguiente forma:

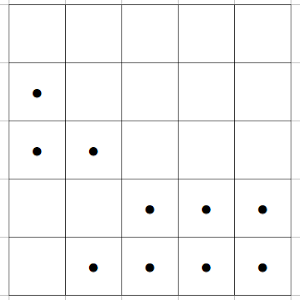
Vamos a ver un par de ejemplos más. Para m = 6, sí es posible ampliar el tablero de m = 5, añadiendo una fila más totalmente ocupada.

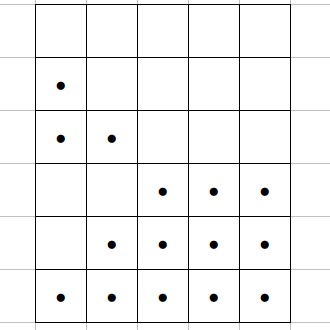
Y, de nuevo, nos encontramos que para m = 7, no es posible rellenar para n = 6, por ser 0 + 1 + … + 5 + 6 = 21 no divisible entre 6, pero sí entre 7, de donde para n = 7, podemos construir una solución con 3 piedras por columna.

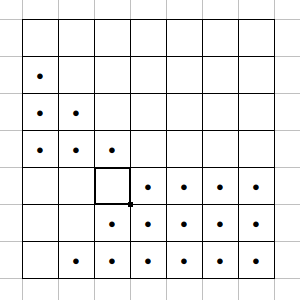
Vale, demostremos que este patrón es correcto ahora.

Una pareja (m, n) será rellenable según las condiciones del problema si n es mayor o igual que m en el caso de que m sea impar, y si n es mayor o igual que m – 1 si m es par.

Según hemos demostrado antes, en el momento en que un tablero de m filas se pueda llenar, tableros con más columnas es posible llenarlos siempre. Por lo tanto, para cada m, hay un tablero de un número mínimo de n columnas que se puede llenar en las condiciones del problema, todos los que tengan un valor de n superior se podrán llenar y todos los que tengan n inferior no podrán llenarse.

Para valores de n inferiores a m – 1, no será posible cumplir las condiciones por que existen exactamente m posibles números entre 0 y m – 1.

Veamos que no es posible encontrar un tablero si m es impar y n = m – 1, pero sí es posible para n = m. Supongamos entonces que m es impar.

La suma 0 + 1 + … + m – 2 + m – 1 es (m – 1)·m/2. Puesto que m es impar, el factor 2 que quitamos será de m – 1, y el número total de factores 2 será uno inferior al de m – 1, por lo que no será posible dividirlo entre el número de columnas. Luego es imposible cumplir las condiciones del problema.

Sin embargo, si el número de columnas coincide con m, podemos situar (m – 1)/2 piedras seguidas en la primera columna, dejando vacía la primera fila. En a siguiente columna repetiremos, dejando una fila más vacía y poniendo esa piedra en la última, en la siguiente dos más, y así sucesivamente, hasta que nos quedemos sin piedras en las primeras (m – 1)/2 + 1 filas, a partir de esa columna situaremos las piedras todas en las columnas inferiores. De esta forma, la primera fila tendrá 0 piedras, la segunda 1, y así hasta la fila (m – 1)/2 + 1, que tendrá (m – 1)/2. La siguiente, puesto que a partir de la columna (m – 1)/2 + 1 tendrá piedras hasta la (m – 1), tendrá (m – 1)/2 + 1 piedras, y cada fila tendrá una piedra más, hasta la última, que tendrá exactamente m – 1.

Ahora, por último, si m es par, sí es posible completar un tablero de m – 1 columnas, tomando el tablero completo (m – 1) por (m – 1) y añadiendo una fila totalmente rellena.

Ha sido un problema muy manipulativo, pero que se ha revelado muy difícil, ya que ha sido uno de los que menos puntuación media se ha obtenido, al menos en mi Fase Local.