Problema 5 de la Fase Local de la Olimpiada Española de Matemáticas 2021
Se dirige a una edad de: 16-17 años

En un torneo de ajedrez participan 8 maestros durante 7 días.

Cada día se disputan 4 partidas en las cuales participan todos los maestros, y al finalizar el torneo todos se han enfrentado contra todos exactamente una vez.

Demuestra que, al terminar el quinto día del torneo, existe un conjunto de al menos 4 maestros que ya han jugado entre ellos todas las partidas.
Solución:

En este problema, la clave es tratar de estudiar lo que sucede en las dos últimas jornadas que quedan, para saber cuáles son los cuatro (al menos) rivales que ya se han enfrentado en las cinco jornadas previas.

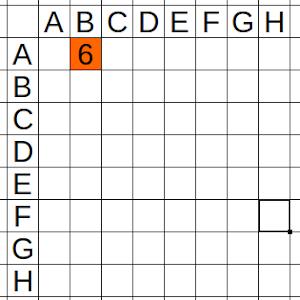
Vamos a hacer una tabla de doble entrada en la que marquemos los que juegan en las últimas jornadas.

La tabla que he usado para ilustrar la entrada representa el orden de una de las posibles formas en las que se desarrolla el torneo, pero puede que no sea la única.

Busquemos un par de jugadores que se enfrenten en la jornada 6 y pongámoslos en la parte alta de la tabla. Les llamaremos A y B.

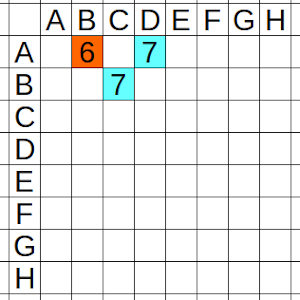
El jugador B no puede repetir con A en la jornada 7, así que C será el jugador que juegue con él, y lo pondremos el siguiente en la tabla. De forma similar, D será el que juegue contra A en esa jornada. Evidentemente, son dos jugadores diferentes.

A partir de aquí, se plantean dos situaciones diferentes. En una de ellas, C y D juegan entre sí en la jornada 6. En ese caso (que llamaremos 1), buscamos otros dos jugadores que jueguen en la jornada 6 y repetimos la situación, llamándoles en este caso E y F, y a los dos nuevos rivales, G y H. Evidentemente, puesto que no queda más gente libre en la jornada 6, Estos dos últimos rivales deben jugar juntos.

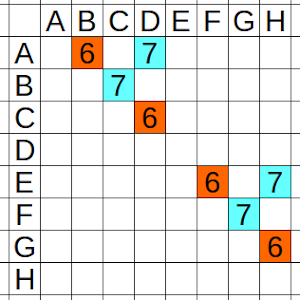
Buscando un poco en la tabla, vemos que en este caso 1, hay varios posibles grupos de 4 maestros que ya han jugado en otras jornadas, por ejemplo A – C – E – G, o B – D – F – H.

Pero podría ser que C y D no jugasen entre sí en la jornada 6 (caso 2), puede ser que cada uno de ellos juegue con un maestro diferente, que no puede ser ni A ni B. Pongamos que C juega contra E y D contra F. Evidentemente, G y H deben jugar juntos en esta jornada, porque son los únicos libres.

Ahora bien, puesto que G y H juegan en la jornada 6, y en la 7 ya están ocupados A, B, C y D, o bien G juega con E y H con F (caso 2.1), o bien G juega con F y H con E (caso 2.2).

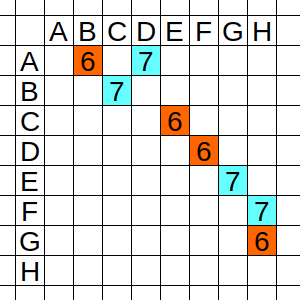
En el caso 2.1, explorando un poco, tenemos que A – C – F – G también han jugado todo ya.

En el caso 2.2, sólo hay que buscar para ver que A – C – F – H ya han jugado todos los partidos.

Con lo cual, queda probado que en todos los casos existe ese grupo de cuatro maestros que ya han jugado todos sus partidos entre ellos.