Problema 7 de la Fase Local de la Olimpiada Española de Matemáticas 2021
Se dirige a una edad de: 16-17 años

Demostrar que todos los números racionales pueden expresarse como suma de algunas fracciones de la forma (n – 1)/(n + 2), con n >= 0 entero, admitiendo repetir sumandos.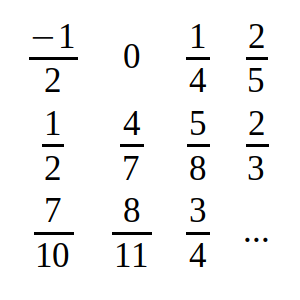
Solución:

Por abreviar, llamaremos a la secuencia de números según su valor de n A(0), por ejemplo, será (0 – 1)/(0 + 2) = -1/2, A(1) = 0, A(2) = 1/4, etcétera.

Así, en la secuencia vemos que, puesto que el denominador siempre es 3 unidades mayor que el numerador, en el caso de que uno de ellos sea múltiplo de 3 (como pasa por ejemplo para a(4)), se puede simplificar la fracción. Sin embargo, cuando no es así, la fracción es irreducible, ya que cualquier múltiplo común debería ser múltiplo también de la diferencia, que es 3.

Por tanto la sucesión de fracciones que necesitaremos está compuesta por {-1/2, 0, 1/4, 2/5, 1/2, 4/7, 5/8, 2/3, 7/10, 8/11, 3/4, 10/13, 11/14, …}

Lo primero que hacemos es jugar con las fracciones primeras de la secuencia para poder generar mediante sumas los números más sencillos.

Por ejemplo, usando A(4) = 1/2, podemos construir 1, y mediante sumas sucesivas todos los enteros positivos. El 0 forma parte de la secuencia (A(1)), y, puesto que tenemos A(0) = -1/2, podemos también construir -1 y todos los enteros negativos.

Así, es suficiente ver que podemos construir las fracciones positivas, y, a partir de éstas, sumando -1 las veces que sea necesario, todas las negativas.

De hecho, basta ver que podemos construir las fracciones de la forma 1/b, ya que sumándolas a veces podemos construir a/b.

Lo más complicado es construir 1/b, para lo cual nos podemos fijar que 1/2 está en la secuencia (A(4)), 1/3 lo podemos construir usando A(7) + A(7) + A(0) + A(0) = 2/3 + 2/3 + (-1/2) + (-1/2).

Para 1/4, podemos hacer dos cosas diferentes. Usar directamente el término A(2), que es ese valor, evidentemente, o bien usar A(10) que es 3/4 y sumarlo 3 veces hasta lograr 9/4, y añadirle 4 veces el término A(0). Cuando veamos el patrón, entenderemos por qué hago esto.

Para 1/5, pasa algo similar. Puedo usar A(3), que es 2/5, sumando 3 veces hasta lograr 6/5 y sumar luego dos veces A(0), pero también puedo ir al A(13),que es 12/15 = 4/5, sumando 4 veces hasta lograr 16/15, y después sumar A(0) 6 veces. Aunque parezca más difícil, el patrón va a ser más claro luego.

El número 1/6 es más difícil de lograr, ya que en la lista que tenemos no sale ningún elemento de denominador 6. De hecho, no sale hasta el A(16) = 15/18 = 5/6, que si lo sumamos 5 veces nos da 25/6 y si le sumamos 8 veces A(0) nos hace obtener el resultado deseado.

Veamos si lo podemos generalizar ahora.

Supongamos que queremos lograr la fracción 1/k para un cierto valor k > 1. Por lo que hemos visto, parece que debemos partir siempre de una fracción que tiene el triple de denominador, así que tendremos A(3k – 2) = (3k – 2 – 1)/(3k – 2 + 2) = (3k – 3)/(3k) = (k – 1)/k.

Ahora, parece que el siguiente paso será sumar la fracción k – 1 veces, obteniendo (k – 1)²/k = (k² – 2k + 1)/k = k – 2 + 1/k, ya que la primera parte de la suma es divisible entre k.

Evidentemente k – 2 es un número entero positivo, sumando 2k – 4 veces (el doble de k – 2) A(0), esta parte de la expresión desaparece se simplifica y obtenemos, en efecto, 1/k.

Seguramente en muchos casos hay métodos sumando menos fracciones, pero seguro que no son tan generales.

Por ejemplo, las fracciones 1/k que no tengan un múltiplo de 3 en el denominador se puede emplear la fracción A(k – 2), que seguro que se puede trabajar con muchas menos. Como (k – 3)/k tiene numerador y denominador mutuamente primos, existe un par de números a y b de forma que a(k – 3) – bk = 1 (debido a que 1 es el máximo común divisor) y por tanto si sumas a veces la fracción tendrás a(k – 3)/k = (bk + 1)/k = b + 1/k, que luego le sumas 2b veces A(0) y da 1/k.

Pero para las fracciones que sean de la forma 1/k con k múltiplo de 3 creo que la forma más sencilla de obtenerlas sería la que hemos encontrado.