Dados especiales
Problema 2 del nivel A fase autonómica de la Olimpiada de la Comunidad Valenciana 2019 Se dirige a una edad de: 12-13 años
Teníamos que decidir quién pedía al profesor de matemáticas que nos dejara estudiar en clase para el examen de inglés que teníamos después, pero nadie se atrevía.
En ese momento, Joan sacó un par de dados cúbicos del bolsillo y dijo: “Cada uno que elija un número, yo voy tirando los dados y cuando coincida la suma de los dos con uno de los números elegidos, tendremos mensajero”.
Le contesté que no era justo, ya que hay sumas como el 7 que salen de muchas más maneras que otras como el 12.
Sin embargo, dijo que eso no pasaba con sus dados. Nos los tuvo que enseñar para que le creyéramos.
¿Sabrías decirnos qué números aparecen en cada una de las caras de los dos dados, si te digo que se podía obtener cualquier suma entre el 1 y el 36, y que todos eran números naturales?

Solución: Aquí.
Solución a bumerán
Problema 2 del nivel B fase autonómica de la Olimpiada de la Comunidad Valenciana 2019 Se dirige a una edad de: 14-15 años
En un cuadrilátero ABCD, cóncavo en D, se tiene que CD = DA = AB, y que el ángulo en A (β) es el doble que el ángulo en C (α), es decir β = 2α.
Calcula la medida del ángulo en B, en función de α.
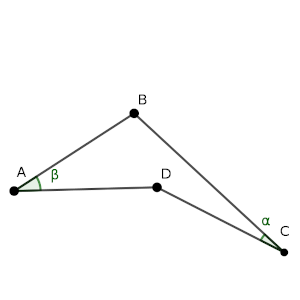
Solución:
(more…)
Bumerán
Problema 2 del nivel B fase autonómica de la Olimpiada de la Comunidad Valenciana 2019 Se dirige a una edad de: 14-15 años
En un cuadrilátero ABCD, cóncavo en D, se tiene que CD = DA = AB, y que el ángulo en A (β) es el doble que el ángulo en C (α), es decir β = 2α.
Calcula la medida del ángulo en B, en función de α.

Solución: Aquí.
Solución a dados
Problema 1 del nivel C fase autonómica de la Olimpiada de la Comunidad Valenciana 2019 Se dirige a una edad de: 10-11 años
Tenemos dos dados, en las caras de uno de ellos aparecen los números 2, 4, 8, 16, 32 y 64, mientras que en las caras del otro aparecen los números del 1 al 6.
Tiramos los dados y multiplicamos los dos números que obtenemos.
¿Cuál es la probabilidad de que esta multiplicación sea un cuadrado perfecto?

Solución:
(more…)
Dados
Problema 1 del nivel C fase autonómica de la Olimpiada de la Comunidad Valenciana 2019 Se dirige a una edad de: 10-11 años
Tenemos dos dados, en las caras de uno de ellos aparecen los números 2, 4, 8, 16, 32 y 64, mientras que en las caras del otro aparecen los números del 1 al 6.
Tiramos los dados y multiplicamos los dos números que obtenemos.
¿Cuál es la probabilidad de que esta multiplicación sea un cuadrado perfecto?

Solución: Aquí.
Solución a área sombreada
Problema 1 del nivel A fase autonómica de la Olimpiada de la Comunidad Valenciana 2019 Se dirige a una edad de: 12-13 años
¿Qué fracción representa la parte sombreada?
En el dibujo, a partir de un cuadrado, se ha dividido cada lado en tres partes, uniendo una esquina con la más lejana de las dos divisiones de los dos lados contrarios, y las dos divisiones más próximas de la otra esquina.
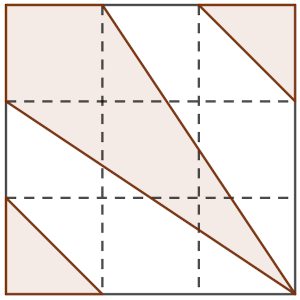
Solución:
(more…)
Área sombreada
Problema 1 del nivel A fase autonómica de la Olimpiada de la Comunidad Valenciana 2019 Se dirige a una edad de: 12-13 años
¿Qué fracción representa la parte sombreada?
En el dibujo, a partir de un cuadrado, se ha dividido cada lado en tres partes, uniendo una esquina con la más lejana de las dos divisiones de los dos lados contrarios, y las dos divisiones más próximas de la otra esquina.

Solución: Aqui.
Solución a el valor de un polinomio
Problema 1 del nivel B fase autonómica de la Olimpiada de la Comunidad Valenciana 2019 Se dirige a una edad de: 14-15 años
Sabiendo que el valor numérico del polinomio p(x) = x² – 3x + 5 en el punto x = k es 0, calcula el valor que tendrá q(x) = x⁴ – 6x³ + 9x² – 7 en el punto x = k.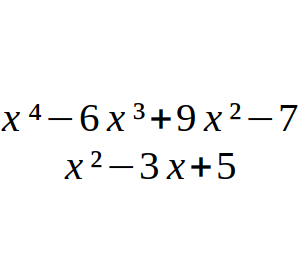
Solución:
Este problema consistía realmente en calcular el valor del polinomio q sin conocer el valor de k.
Si buscamos el valor de k, nos encontraremos que no es un número real (según nuestros conocimientos, no existirá) y en ese caso, puede que caigamos en la tentación de dar el problema por cerrado. Sin embargo, a pesar de no ser un número real, se puede evaluar el polinomio q a partir de propiedades como que p(k) = 0, en este caso.
La clave es ver si el polinomio p está contenido en el polinomio q un determinado número de veces, y para eso la herramienta que debemos usar es la división:
Si dividimos q(x) = x⁴ – 6x³ + 9x² – 7 entre p(x) = x² – 3x + 5, veremos que realmente x⁴ – 6x³ + 9x² – 7 = (x² – 3x + 5)( x² – 3x – 5) + 18.
Eso quiere decir que, si k hace que p(k) valga cero, en realidad el producto que forma el primer sumando es cero, con lo que el polinomio q(k) realmente valdrá 18.
En este problema veo algunas cosas que resultan poco adecuadas para un concurso, ya que dependiendo de lo que la persona que se enfrenta a él sepa, puede tratar de hacer una cosa u otra, y además debe estar familiarizado con la operación de división entre polinomios para darle respuesta, ya que no se me ocurre ningún otro método para darle respuesta.