Problema 2 del nivel B fase autonómica de la Olimpiada de la Comunidad Valenciana 2019 Se dirige a una edad de: 14-15 años
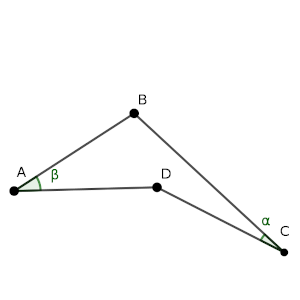
En un cuadrilátero ABCD, cóncavo en D, se tiene que CD = DA = AB, y que el ángulo en A (β) es el doble que el ángulo en C (α), es decir β = 2α.
Calcula la medida del ángulo en B, en función de α.
Solución:
Es un problema al que hay que dar muchas vueltas. Lo primero es intentar construir este dibujo, usando los datos que nos dan. El que aparezca un ángulo y su doble es clave, ya que sugiere que hay un punto en el centro de una circunferencia y otro en el borde, ya que desde un punto de la circunferencia a dos puntos de la misma se forma un ángulo mitad que desde el centro.
En un principio traté de usar triángulos isósceles, pero siempre faltan ángulos por completar.
Aquí hay un triángulo equilátero escondido, aunque no lo parezca. Si se hace el simétrico de A respecto a la recta BD, le llamamos F, tenemos el centro de una circunferencia que contiene a C, puesto que su ángulo es la mitad que el que hay desde ese punto F.
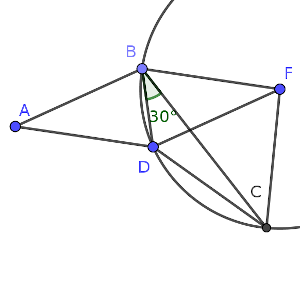
Ahora, como el radio de la circunferencia es el mismo que la distancia DC, se forma un triángulo equilátero entre F, D y C. Por eso, el triángulo FDC tiene todos sus ángulos de 60º, y por eso el ángulo que se forma entre CB y BD mide la mitad, es decir, 30º.
Puesto que el ángulo ABD pertenece a un triángulo equilátero de ángulo desigual 2α, mide 90 – α, para que entre los tres sumen 180º (es igual al ADB).
Y por lo tanto, ABC, que es la suma de ABD + DBC, mide exactamente 120 – α.