Problema 4 del nivel A fase autonómica de la Olimpiada de la Comunidad Valenciana 2019
Se dirige a una edad de: 12-13 años

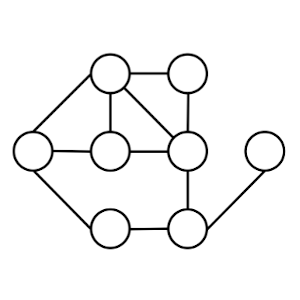
Coloca los números del 1 al 8 en los círculos de la imagen de forma que la suma de todos los números que están directamente conectados por una línea con uno determinado, sin contar el propio número, suma lo que indica la siguiente relación.

Los que están conectados con el 1 suman 10.

Los que están conectados con el 2 suman 20.

Los que están conectados con el 3 suman 15.

Los que están conectados con el 4 suman 13.

Los que están conectados con el 5 suman 21.

Los que están conectados con el 6 suman 3.

Los que están conectados con el 7 suman 8.

Los que están conectados con el 8 suman 14.

Solución:

La estrategia fundamental es buscar aquellos que menos conexiones tienen. Vemos que uno de los círculos tiene una única conexión, luego el número que esté en ese círculo, será el mismo que la suma de los conectados. Vemos que no hay más remedio que sea el 6 y esté conectado con el 3, ya que la otra opción es que fuese el 7 estuviese conectado con el 8, pero en ese caso al otro lado debería haber otro 7, lo que es imposible.

Después de ésto, los números conectados al 3 deben sumar 9. Tenemos las posibilidades 1 – 8, 2 – 7 y 4 – 5. Sin embargo, pocos de ellos pueden ocupar el lugar que sólo está conectado con el 3 y con otro.

Si intentamos poner el 8, no puede ser porque habría que poner un 11 en la otra conexión (imposible).

Con el 2, habría que poner un 17 (no puede ser tampoco).

Con el 4, habría que usar un 10 (no puede ser).

Y con el 5 un 18. También es imposible.

Ahora, hay que decidir entre el 1 y el 7.

Si tratamos de poner el 7, descubrimos que este número deberá estar conectado al 5 y al 3, pero el 5 debe estar conectado a una suma de 21 y tiene un 7 conectado, por lo que las otras dos deben sumar 14. No hay forma de hacerlo sin usar un número repetido, ya que 14 sólo se puede obtener sumando 8 y 6.

Luego debemos poner un 1. En la otra casilla conectada con el 3 hay que poner un 8. Y conectado al 1, un 7.

Sólo nos queda por poner el 2, el 4 y el 5.

Puesto que todos ellos están conectados con el 8, no nos da ninguna pista (suman entre los tres y el 3 14, como era de esperar). Pero hay dos de ellos conectados al 7, que deben sumar 7 para que entre los tres conectados sumen 8. Por lo tanto el 2 y el 5 están conectados al 7 y el 4 no.

Ahora es evidente que el 5 debe ir conectado al 4 (para que sumen 13 sus conectados) y el último será el 2.

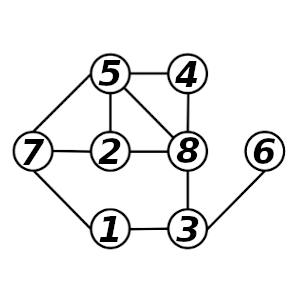
Estuve planteando el problema en clase (¡gracias, Juan Pablo y Noa por vuestra realimentación acerca de la solución!) y fue bastante entretenido para todos los que intentaron resolverlo.