Problema 1 de la fase nacional de la 57 Olimpiada Matemática Española (2021)
Se dirige a una edad de: 16-17 años

Los vértices A, B y C de un triángulo equilátero de lado 1 están en la superficie de una esfera de radio 1 y centro O.

Sea D la proyección ortogonal de A sobre el plano α, determinado por B, C y O.

Llamamos N a uno de los cortes con la esfera de la recta perpendicular a α por O.

Halla la medida del ángulo DNO.

(Nota: la proyección ortogonal de A sobre el plano α es el punto de corte con α de la recta que pasa por A y es perpendicular a α.)

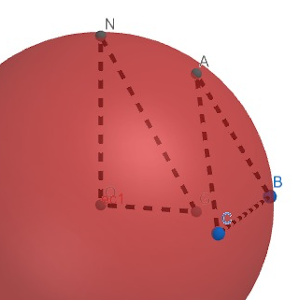
Solución:

En este problema, lo más importante es la visualización de los puntos. Si tenemos problemas con esto, deberemos recurrir al uso de coordenadas.

Lo principal es que A, B, C y O están todos a una unidad de distancia, es decir, ocupan los vértices de un tetraedro regular de lado 1.

Si usamos coordenadas, vamos a situar O en el (0, 0, 0). Así, todos los puntos de la esfera (A, B, C y N) cumplirán que la suma de sus coordenadas al cuadrado valen 1.

Puesto que el plano OBC, α, es importante en el problema, tomaremos el plano horizontal, es decir, que serán los puntos cuya coordenada z vale cero, y las rectas perpendiculares serán aquellas en las que todos los puntos tienen una misma x y una misma y, variando sólo la z.

Ahora, para elegir las coordenadas de los puntos B y C, voy situarlos de forma que sean simétricos respecto al eje X, así que tendrán las coordenadas (x, y, 0) y (x, -y, 0), de forma que x² + y² = 1. Puesto que la distancia entre ambos, 2y = 1, tenemos que y = 1/2 y x = raíz(3)/2.

Así, tenemos que O = (0,0,0), B = (raíz(3)/2, 1/2, 0) y C = (raíz(3)/2, -1/2, 0). Para determinar A, tendremos en cuenta que su y vale 0 para que esté a la misma distancia de B y de C, así que será de la forma (x, 0, z), cumpliendo que su distancia a O es 0 (x² + z² = 1) y su distancia a B y a C vale 1 también, es decir, (x – raíz(3)/2)² + 1/4 + z² = 1. De ese par de ecuaciones deducimos que z² = 1 – x², por lo que (x – raíz(3)/2)² + 1/4 + 1 – x² = 1. Quitando paréntesis, tenemos que x² – raíz(3)x + 3/4 + 1/4 – x² = 0, es decir, que – raíz(3)x + 1 = 0. Por tanto, x = 1/raíz(3), es decir que x = raíz(3)/3. Y z = raíz(6)/3 (se puede suponer, sin pérdida de generalidad, que es positiva).

Por tanto A = (raíz(3)/3, 0, raíz(6)/3), B = (raíz(3)/2, 1/2, 0) y C = (raíz(3)/2, -1/2, 0). Se puede comprobar que con esas coordenadas se cumplen todas las condiciones de la situación propuesta.

La proyección de A sobre el plano sería eliminarle la coordenada z, es decir, que D = (raíz(3)/3, 0, 0), y El punto N puede ser tanto (1, 0, 0) como (-1, 0, 0). Por comodidad, supondremos que usamos el (1, 0, 0), aunque el resultado es el mismo.

El triángulo NOD es rectángulo en O, claramente, y entonces el ángulo que buscamos, el que se forma en N, tiene una tangente que sería el resultado de dividir DO entre NO, es decir, que su tangente sería raíz(3)/3, es decir, que el ángulo buscado sería el de 30º, que es el único que tiene esa tangente y cabe en un triángulo rectángulo.