Problema 4 de la fase nacional de la 57 Olimpiada Matemática Española (2021) Se dirige a una edad de: 16-17 años
Sean a, b, c y d números reales tales que a + b + c + d = 0 y a² + b² + c² + d² = 12.
Halla el valor mínimo y el valor máximo que puede tomar el producto abcd, y determina para qué valores de a, b, c y d se consiguen ese mínimo y ese máximo.
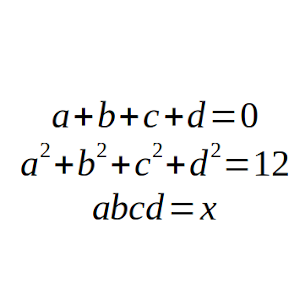
Solución: Aquí.