Problema 3 del nivel C fase comarcal de Alicante de la Olimpiada de la Comunidad Valenciana 2021
Se dirige a una edad de: 10-11 años

A la figura formada por dos triángulos equiláteros unidos por un lado se le llama diamante.

Averigua cuántos pentamantes (agrupaciones de 5 triángulos equiláteros unidos todos ellos con otro por alguno de sus lados) hay, y si algunos de ellos puede teselar un plano.

Entendemos por teselar cubrir una superficie plana con un patrón regular sin que se superpongan ni dejen huecos. Se puede teselar con cuadrados, triángulos de todo tipo, hexágonos regulares, etc…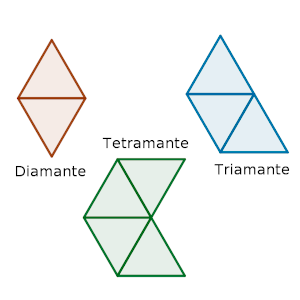
Solución:

Este ejercicio es muy creativo, se trata de encontrar, mediante ensayo, todas las posibilidades para unir cinco triángulos equiláteros.

Es evidente que sólo hay un tipo de diamante, ya que si unes dos triángulos por un lado, sólo puede quedar una figura (ese tipo de rombo que aparece en el ejemplo).

De la misma forma, si unes ese rombo con un nuevo triángulo equilátero, sólo puede quedar una figura, que es la que forma el “triamante”, esa especie de trapecio.

Pero en realidad a partir de aquí, la cosa se complica, ya que hay tres tipos de tetramante, formado a partir de unir un triángulo equilátero al triamante. Veamos el aspecto que tiene cada uno de ellos, según que lo añadas en la base larga, en la corta, o en uno de los lados no paralelos a las bases.

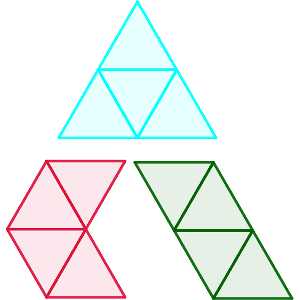
Ahora, tenemos más diversidad para elegir uno de ellos y añadirle un nuevo triángulo equilátero.

La simetría del que tiene forma de triángulo sólo permite construir un nuevo tipo de figura a partir de él.

Sin embargo, la que procede de poner un triángulo en la base grande, si evitamos volver a repetir la que proviene del triángulo, nos quedan dos opciones: poner el triángulo en la otra parte de la base del trapecio original, o en uno de los lados no paralelos (en el otro, vuelve a aparecer el triángulo).

Por último, en la pieza que ampliaba el trapecio por el lado para formar un paralelogramo, sólo podemos alargarlo a ser otro trapecio si no queremos repetir una de las anteriores.

En total, podemos crear 4 figuras diferentes, conocidas como pentamantes.

Ahora, vamos a tratar de descubrir si podemos teselar el plano con ellas o no.

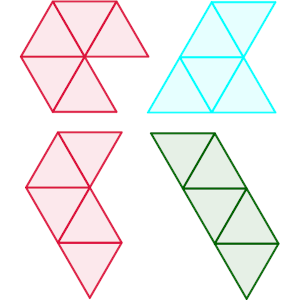
Es evidente que con la que tiene forma de trapecio sí es posible, ya que podemos hacer tiras largas unidas.

Otra que no es difícil entender cómo puede funcionar es la que parece casi un hexágono, ya que se pueden encajar dos para construir un módulo similar a un hexágono alargado, y teselar el plano con él.

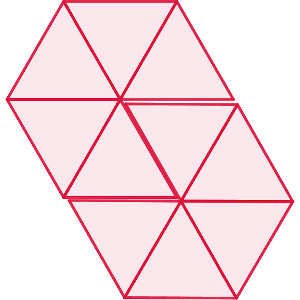
La otra figura alargada es algo más compleja. A mí se me ocurrió poner varias en paralelo, y después otras giradas 180º, de forma que encajaran como una cremallera.

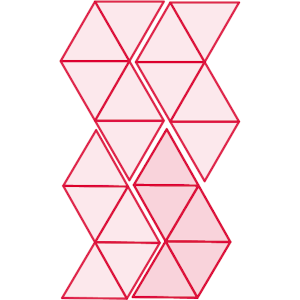
Por último, la pieza que queda me parece mucho más difícil, pero también es posible teselar con ella. Sin embargo, es difícil explicarlo sin aportación gráfica. Se trata de combinarlas de dos en dos y sacar una fila con escalones, para luego unirla a otra idéntica.