Problema 3 del nivel B fase comarcal de Alicante de la Olimpiada de la Comunidad Valenciana 2021
Se dirige a una edad de: 14 -15 años

A partir del triángulo equilátero rojo, que tiene un área de 10 cm², se prolongan los segmentos del mismo hasta que alcanzan una longitud igual al doble de su longitud original, obteniendo los puntos A’, B’ y C’.

¿Cuál será el valor del área del nuevo triángulo equilátero que se forma?

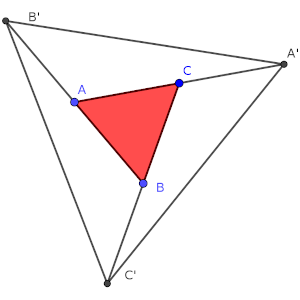
Solución:

La geometría suele ser uno de esos apartados que más se resisten dentro de este nivel.

Hay varias formas de hacerlo, algunas de las cuales incuyen formas muy imaginativas de completar el dibujo para que se pongan de manifiesto las proporciones adecuadas.

La que veo más fácil de entender es calcular el área de uno de los tres nuevos triángulos que se han añadido a la imagen.

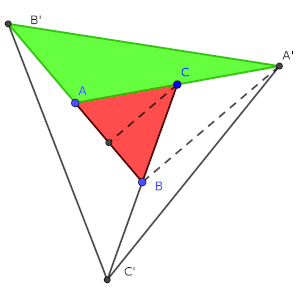
Si observamos el triángulo (en la imagen en verde) B’AA’, tenemos que su base B’A mide lo mismo que la original, mientras que su altura sobre esta base mide exactamente el doble que la del ABC.

Es curioso que, por construcción, el pie del triángulo coincide exactamente con el punto B, debido a la simetría que implica que la altura divida al triángulo en dos partes exactamente iguales, aunque en realidad no es necesario para que se cumpla la proporción.

Puesto que el área de un triángulo es la mitad de la base por la altura, el área del triángulo verde mide el doble que la del original, es decir, 20 cm².

Y eso quiere decir que el área del triángulo grande A’B’C’ mide 10 + 20·3 = 70 cm².

En realidad, el razonamiento no requiere que el triángulo original sea equilátero, cualquier triángulo que se hubiese usado tiene esta misma propiedad, aunque el triángulo resultante normalmente no será semejante al triángulo de partida.