Problema 0 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Calcula cuántos números enteros son solución de la siguiente inecuación:
|2021 – |x|| ≤ 2022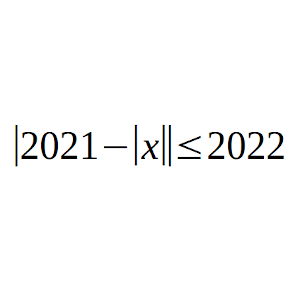
Solución:
Como en muchas otras ocasiones, el problema 0 de la Olitele tiene como solución un número entero, de forma que pueda hacerse la corrección de forma automática.
Hay varias formas de abordar el problema. La más automática que se me ocurre es buscar dónde se da la igualdad, y puesto que la función valor absoluto es continua, podremos buscar en qué intervalos es cierta la desigualdad, y contar después la cantidad de enteros.
Si consideramos la igualdad |2021 – |x|| = 2022, puesto que el valor absoluto puede o no cambiar el signo de lo que contiene, podríamos ver dos casos.
Si no cambia el signo, tenemos que 2021 – |x| = 2022, con lo que 2021 – 2022 = |x|, es decir, |x| = -1, lo cual es imposible.
Si cambia de signo, tendremos que |x| – 2021 = 2022, por lo que |x| = 4043. Y puesto que este valor absoluto puede cambiar o no el signo, tenemos dos soluciones, x = 4043 y x = -4043.
Sin embargo, de los tres intervalos en los que este par de números divide la recta real, el único que cumple la desigualdad, como se puede comprobar fácilmente, es el intervalo entre -4043 y 4043, que comprende a ambos pues la desigualdad no es estricta.
El total de números enteros que hay en este intervalo sería realmente 8087, 4043 positivos, 4043 negativos, y el 0.