Problema 7 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
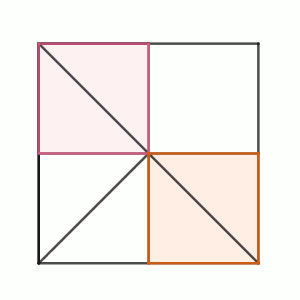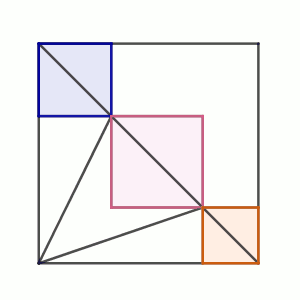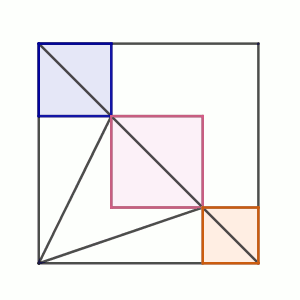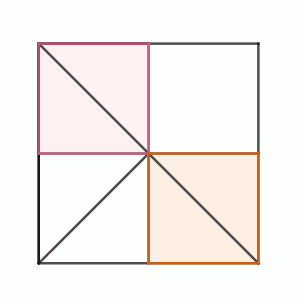
Sobre la diagonal de un cuadrado se sitúan dos puntos que se usan para construir tres cuadrados de forma que el cuadrado central tiene la misma área que la suma de las otras dos.
Razona con todo detalle y precisión cuánto mide el ángulo que se forma en un vértice del cuadrado contenedor que no esté en la diagonal al unirlo con los dos vértices de la diagonal del cuadrado central.
Solución:
Seguro que hay otras maneras, pero lo que más trabajamos a estos niveles es la geometría algebraica, así que voy a hacer depender todo de dos variables, y tratar de poner en función de ellas los elementos clave del dibujo.
Puesto que el tamaño del cuadrado no es relevante (si fuese más grande podría escalarse la imagen), trabajaremos sin pérdida de generalidad sobre el cuadrado de vértices (0,0), (1,0), (1,1) y (0,1).
La diagonal de construcción, por ejemplo, será la que va de (0,0) a (1,1), por lo que todo estará en elegir dos puntos a, b, sobre esta diagonal (a, a) y (b, b) serán las coordenadas de los puntos. Las primeras condiciones básicas en este contexto es que 0 < a < b< 1.
Ahora debe darse la coincidencia de áreas, por lo que a² + (1 – b)² = (b – a)², es decir, que a² + b² + 1 – 2b = a² + b² – 2ab, lo que nos lleva a que 1 + 2ab – 2b = 0, lo que es una condición que relaciona a con b. También podemos escribirla, por si acaso, viendo que 1 = 2b – 2ab = 2b(1 – a), como que en realidad b = 1/(2(1 – a)), lo que nos puede venir bien.
Se comprueba que, en efecto, para todo valor de a entre 0 y 1, se da que a² + (1 – 1/(2(1 – a)))² es igual que (1/(2(1 – a))² – a)², sencillamente desarrollando y viendo que todos los sumandos son idénticos. En realidad, para que la construcción pueda hacerse, el valor de a debe ser menor que ½.
Ahora, para encontrar el ángulo que buscamos, hay varias estrategias.
La de utilizar el producto escalar fue la primera en la que pensé, pero da más problemas por el módulo. Otra es trabajar con pendientes.
Lo primero que necesitamos es los vectores que corresponden a unir un vértice (podríamos usar el (1, 0) o el (0,1), yo voy a usar el (1, 0)) con los puntos (a, a) (vector (a – 1, a)) y con el punto (b, b) (vector (b – 1, b)).
Si razonamos por pendientes, la pendiente del primero es a/(a – 1) y la del segundo es b/(b – 1), y, puesto que la pendiente es la tangente del ángulo con la horizontal, la tangente del ángulo comprendido entre ambos sería (m – n)/(1 + mn), en este caso la tangente sería (a/(a – 1) – b/(b – 1))/(1 + ab/((a – 1)(b – 1))). Multiplicando por los denominadores, tendríamos (a(b – 1) – b(a – 1))/ ((a – 1)(b – 1) + ab)) = (b – a)/(2ab – a – b + 1).
Para conocer en detalle el valor que tiene esta tangente (que, puesto que el ángulo está comprendido entre 0 y 90º nos determinará perfectamente qué ángulo es), usamos ahora que b = 1/(2(1 – a)).
Y nos queda que la tangente es (1/(2(1 – a)) – a)/(2a/(2(1 – a)) – a – 1/(2(1 – a)) + 1), lo que de nuevo nos obliga a quitar denominadores multiplicando por 2(1 – a) en numerador y denominador, así que queda la expresión (1 – 2a(1 – a))/(2a – 2a(1 – a) – a – 1 + 2(1 – a)) = (1 – 2a(1 – a))/(2a – 2a(1 – a) – a – 1 + 2 – 2a)) = (1 – 2a + 2a²)/(1 – 2a + 2a²) = 1.
Luego el ángulo no depende de a, siempre es 45º, ya que es el único entre 0 y 45º que tiene tangente 1.
Si razonamos por producto escalar, también es posible, ya que el módulo del primer vector sería raíz(2a² – 2a + 1), y el del segundo, raíz(2b² – 2b + 1), y el producto escalar sería ab + ab – a – b + 1 = 2ab – a – b + 1.
Como sabemos que b depende de a, tenemos que el módulo seguiría siendo raíz(2a² – 2a + 1) en el primer caso, pero en el segundo sería raíz(2/(4(1 – a)²) – 1/(1 – a) + 1) = raíz((2 – 4(1 – a) + 4(1 – a)²)/(2(1 – a)) = raíz(4a² – 4a + 2)/(2(1 – a)). Y el producto sería a/(1 – a) – a – 1/(2(1 – a)) + 1 = (2a – 2a(1 – a) – 1 + 2(1 – a))/(2(1 – a)) = (2a² + 2a + 1)/(2(1 – a)).
Para calcular entonces el coseno del ángulo que forman (que de nuevo nos determinará el ángulo entre 0 y 90º), dividiremos el producto escalar entre el producto de los módulos, obteniendo la expresión ((2a² + 2a + 1)/(2(1 – a)))/(raíz(2a² – 2a + 1)raíz(4a² – 4a + 2)/(2(1 – a))) = (2a² + 2a + 1)/(raíz(2a² – 2a + 1)raíz(4a² – 4a + 2)).
Ahora, si tenemos en cuenta que las raíces son iguales excepto un valor 2, tenemos que ese coseno valdría (2a² + 2a + 1)/((2a² + 2a + 1)raíz(2)) = 1/raíz(2), con lo que realmente de nuevo obtenemos que el ángulo que forman es 45º.
El proceso, en este caso, es más laborioso por implicar las raíces cuadradas.