Problema 2 de la Fase Local de la Olimpiada Española de Matemáticas 2022 (viernes tarde) Se dirige a una edad de: 16-17 años
Sea ABCD un cuadrilátero convexo, y sea P un punto en su interior.
Si se cumple que área(PAB)·área(PCD) = área(PBC)·área(PDA), demostrar que el punto P se encuentra en el segmento AC o en el segmento BD.
Solución:
Este problema me ha tenido ocupado bastante tiempo para prepararlo en condiciones. Pondré dos soluciones, una basada en conocimientos geométricos básicos, y otra usando coordenadas, junto con una pequeña explicación de cómo preparo yo algunas de las deducciones en este campo.
La idea base en ambos casos es ver que, si suponemos que P no cumple las condiciones de estar en uno de los dos segmentos de las diagonales, entonces la igualdad de áreas no se puede alcanzar o tiene consecuencias imposibles (reducción al absurdo).
Partiendo de conocimientos básicos en geometría, vemos que las áreas de los triángulos no pueden expresarse de una forma común tal y como están en la igualdad inicial, debido a que los dos pares de triángulos cuyas áreas se multiplican no tienen nada en común. Para poder empezar a trabajar, vemos que hace falta expresar la igualdad de otra forma equivalente, por ejemplo como área(PAB)/área(PDA) = área(PBC)/área(PDC).
Una vez visto así, ya tenemos un lado en común (en ambos casos), así que expresamos el área de PAB como PA·h1/2, y el área de PDA como PA·h2/2. La expresión área(PAB)/área(PDA) es equivalente, puesto que PA y 2 se simplifican, a h1/h2 (ver dibujo).
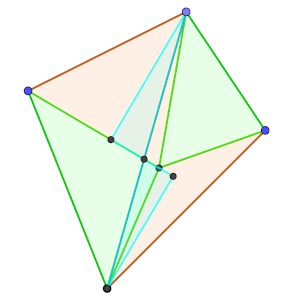
Estos dos segmentos (alturas), si los unimos con la diagonal BD, forman junto con ésta y la prolongación de PA dos triángulos rectángulos semejantes, ya que h1 y h2 son paralelos, y por tanto los segmentos en los que PA o su prolongación corta a la diagonal también guardan la misma proporción. Llamemos E al punto en que PA o su prolongación corta a la diagonal.
Tenemos que EB/ED es entonces igual al cociente área(PAB)/área(PDA) inicial.
Puesto que P no pertenece a la diagonal AC, el segmento PC no es paralelo a PA, por lo que las alturas h3 y h4, de los triángulos PBC y PDC sobre el lado PC no son paralelos, pese a que su proporción es la misma según la igualdad inicial. Además, puesto que P no pertenece tampoco al segmento BD, el segmento PC (o su prolongación) corta a BD en otro punto diferente de E, llamémosle F. Sin embargo, FB/FD debe valer lo mismo que EB/ED, cosa imposible, ya que el cociente XB/XD es estrictamente creciente para los puntos X desde B a D.
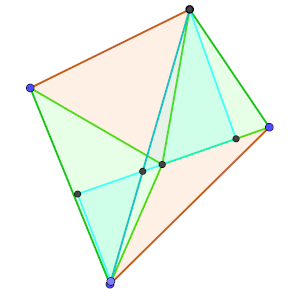
Hemos llegado al absurdo.
Veamos el otro método, exclusivamente algebraico.
Si queremos calcular un área en función de sus coordenadas, necesitamos un método eficaz y rápido. Imaginemos que tenemos tres puntos A(a,b), B(c,d) y C(e,f). Para calcular el área podríamos multiplicar la base AB por la mitad de la altura a la base desde C, pero para calcular la altura debemos hacer uso de la perpendicular.
Vayamos por partes. El vector AB sería (c – a, d – b). Un vector perpendicular podría ser n (b – d, c – a) (observamos que hemos invertido la posición de las dos componentes, y una de ellas se ha cambiado de signo, y encontrar la altura significa multiplicar escalarmente uno de los dos vectores AC o BC (da lo mismo cuál) por n y dividirlo por el módulo de n. Este producto daría (e – a, f – b)·(b – d, c – a)/mod(n) = (eb – de – ab + ad + fc – af – bc + ba)/mod(n) = (eb – de + ad + fc – af – bc)/mod(n). Pero como n y la base tienen el mismo tamaño, al multiplicar para calcular el área se simplifcaría, quedando Área ABC = (eb + ad + fc – af – bc – de)/2.
Puesto que es difícil precisar si el producto va a salir positivo o negativo, hablando en propiedad deberíamos tomarla en valor absoluto. Pero el signo sale igual en todos los triángulos si tomamos los vértices en el mismo sentido (horario o antihorario) y en nuestro problema da lo mismo.
Si uno se fija, podemos calcular el área con las coordenadas, sumando todos los productos entre la primera coordenada de cada vértice y la segunda de su vértice siguiente en sentido antihorario, y restando los productos de la primera coordenada de cada vértice y la segunda de su vértice siguiente en sentido horario. Evidentemente, al final, hay que dividir por 2.
Por ejemplo, el área del triángulo (1,2) (4,0) (2, 3) sería (0 + 12 + 4 – 3 – 8 – 0) = 5/2.
Ahora, puesto que nos interesa si el punto P está o no en las diagonales, uno de los ejes voy a situarlo en la diagonal.
Así, por ejemplo, tenemos que A(0, 0), B(a, b), C(t, 0), D(c,d) y P(x, y). Dadas las condiciones del enunciado, sabemos que t es un número mayor que cero y que y también es distinto de cero (porque si no, P estaría en la diagonal).
El área APB sería xb – ay, mientras que el área CPD sería xd + ty – td – cy.
El área APD sería cy – xd, mientras que el área BPC sería tb + ay – xb – ty.
El primer producto, por tanto, sería x²bd + xybt – xbdt – xybc – xyad – y²at + yadt + y²ac.
El segundo producto sería ybct + y²ac – xybc – y²ct – xbdt – xyad + x²bd + xydt.
Si hacemos la igualdad x²bd + xybt – xbdt – xybc – xyad – y²at + yadt + y²ac = ybct + y²ac – xybc – y²ct – xbdt – xyad + x²bd + xydt, vemos que muchos términos se pueden simplificar, quedando equivalente a xybt – y²at + yadt = ybct – y²ct + xydt.
Puesto que sabemos que t no vale 0, y que y tampoco vale 0, y observamos que todos los términos llevan un factor t y un factor y, podemos eliminarlos, quedando la expresión xb – ya + ad = bc – yc + xd.
Pero sabemos que esa expresión es equivalente a xb – ya + ad – bc + yc – xd = 0. Sorprendentemente, esa expresión, que tiene seis términos, podemos comprobar que es la forma de calcular el área del triángulo BPD, y si vale cero, el significado que tiene es que el punto está alineado con B y con D, lo que es contrario a la hipótesis inicial.
Con lo que está demostrado el enunciado.