Problema 4 de la Fase Local de la Olimpiada Española de Matemáticas 2022 (viernes tarde)
Se dirige a una edad de: 16-17 años

Encuentra todos los polinomios p(x) con coeficientes reales tales que p(x) + p(y) + p(z) + p(x + y + z) = p(x + y) + p(y + z) + p(x + y) para cualquier terna de números reales x, y, z.

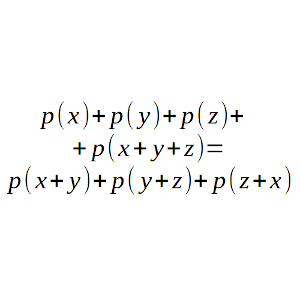
Solución:

En este caso, yo empezaría por trabajar con polinomios de grado bajo para ver qué sucede.

Si probamos con polinomios de grado 1, de la forma p(x) = ax + b, en seguida nos damos cuenta de que para cualquier terna (x, y, z) de números reales, tendríamos que ax + ay + az + ax + ay + az + 4b = ax + ay + ay + az + az + ax + 3b, con lo que b = 0, pero no se aprecia ninguna restricción sobre la pendiente a.

Es sencillo comprobar que los polinomios de la forma p(x) = ax cumplen la relación sea cual sea el valor de a (incluso a = 0). Y ningún polinomio de grado 0, excepto el polinomio 0 la cumple.

Es más, cualquier polinomio que cumpla la relación, va a tener un término independiente nulo (ya que si ponemos x = y = z = 0, tendríamos que 4p(0) = 3p(0), por lo que p(0) = 0.

Por el tipo de relación que tenemos, es sencillo ver que si dos polinomios p y q cumplen la condición, también la cumple cualquier combinación lineal de ambos de la forma s·p(x) + t·q(x), ya que sólo depende de unas sumas.

Por lo tanto, si un polinomio de segundo grado cumple la condición, podremos plantearnos los polinomios de la forma p(x) = x² exclusivamente y ver si cumplen la condición o no.

De esta forma, vemos que en efecto este polinomio cumple la condición, ya que x² + y² + z² + x² + y² + z² + 2xy + 2xz + 2yz = x² + y² + 2xy + y² + z² + 2yz + z² + x² + 2xz. Si no conoces la forma de desarrollar (x + y + z)², es suficiente multiplicar (x + y + z) por esa misma expresión, y verás que coincide con lo que he puesto.

De momento, por tanto, podemos apreciar que los polinomios de la forma ax² + bx cumplen esa condición. Sin embargo, veremos que grados mayores es imposible que la cumplan, y la explicación de por qué sucede no es tan sencilla.

Probar que x³ no lo cumple (y que por lo tanto no hay ningún polinomio de tercer grado que lo cumpla) es relativamente complicado si lo hacemos en función de valores generales x, y, z, y el motivo es que, mientras en el primer extremo de la igualdad aparece un producto de la forma (x + y + z)³, que origina varios términos de la forma xyz, que tendrán factores con las tres variables, mientras que en el segundo extremo no aparece ningún elemento de este tipo.

Sin embargo, es difícil llevar esta propiedad a una de carácter general, salvo que usemos inducción sobre el grado máximo, y, aún así, no sería sencillo.

Sin embargo, usar un valor específico para x, y, z puede darnos una idea.

Supongamos que tenemos un polinomio de la forma a_nxⁿ + a_{n – 1}x^{n – 1} + … + a₀ que cumple la propiedad, y tomemos x = x, y = x y z = -x. La propiedad por tanto pasaría a ser 2p(x) + p(-x) + p(x) = p(0) + p(0) + p(2x), y, puesto que p(0) = 0, según hemos visto, 3p(x) + p(-x) = p(2x).

Supongamos que hay un polinomio de grado mayor que 2 que cumple la relación. Observamos que en el lado izquierdo de la igualdad tendríamos el coeficiente a_n multiplicado a xⁿ por 3 + 1 (o por 3 – 1 si n fuese impar), mientras que en lado derecho tendríamos el coeficiente a_n multiplicado por 2ⁿ. Si restamos ambas desigualdades, obtenemos un polinomio igualado a cero para todos los valores de x, con lo que es un polinomio con todos sus coeficientes nulos. Eso implica que 3 + 1 = 2ⁿ para los valores pares (cosa que sólo sucede en el caso de n = 2), y 3 – 1 = 2ⁿ para los términos de grado impar, lo que implica que n = 1. Eso nos lleva a un absurdo, ya que hemos supuesto que el grado era mayor que 2.

Por lo tanto, los únicos polinomios que cumplen esa condición son los de la forma ax² + bx.