Problema 14 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
Este es el problema de razonamiento que más puntos da del concurso. Se trata de resolver tres problemas similares en los que hay que razonar el área que falta para completar el polígono que se dibuja.
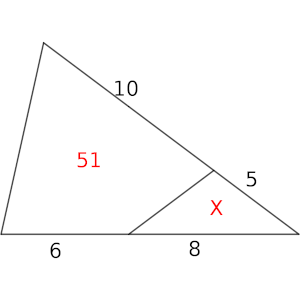
A) Un triángulo se ha descompuesto en dos partes, un cuadrilátero y un triángulo, tal y como se ve en la figura.
Se indican las longitudes de los segmentos en los que se han dividido los lados y el área del cuadrilátero.
Calcula el valor X del área del triángulo.
B)
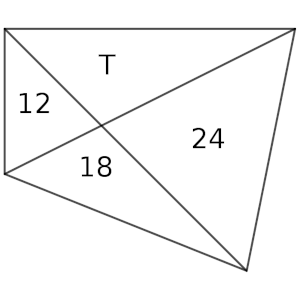
Las dos diagonales de un cuadrilátero lo dividen en 4 triángulos. Si las áreas, tomadas en sentido horario, miden 24, 18, 12 y T, averigua el valor de T.
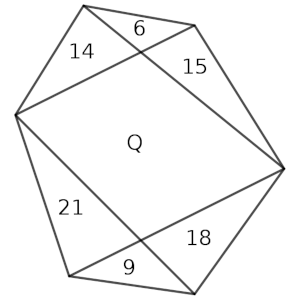
c) En un hexágono se trazan 4 diagonales, de la forma que indica el dibujo, y se ha descompuesto en seis triángulos y un cuadrilátero.
Conocemos las áreas de seis triángulos, que podemos ver en la figura.
Calcula el valor de Q, el área del cuadrilátero.
Solución:
Mi forma de aproximarme a estos problemas será tratar de estudiar las relaciones entre las figuras.
A) En este apartado, usaremos una figura intermedia, en la que tendremos una proporcionalidad típica del teorema de Tales
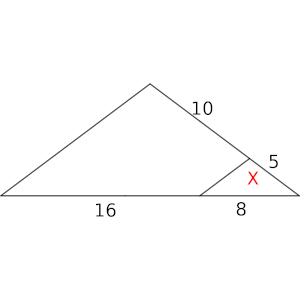
En este caso, las dimensiones del triángulo grande son proporcionales a las del pequeño con un factor de proporcionalidad 3 (los dos lados que prolongan los originales son 3 veces más grandes) por lo que el área será 9x.
Ahora bien, este triángulo tiene la misma altura que el que teníamos en el dibujo original, pero su base es 24, mientras que en el dibujo original, su base era 14.

Por tanto, el triángulo grande del dibujo debe tener un área de 14·9x/24 = 51 + x.
Si simplificamos, tendremos 21x/4 = 51 + x, por lo que 21x = 204 + 4x, y por tanto 17x = 204, de donde x = 12.
B) En este apartado, observo que cada par de triángulos que tienen un lado en común, tienen las áreas proporcionales a sus alturas, y además, si tienen sus bases sobre el mismo segmento, tienen la misma altura.

De esta forma, el triángulo que mide 12 y el que mide 18 tienen la misma altura mirado sobre la base que está en el segmento que forma la diagonal que los separa del que mide T y del que mide 24.
Por otro lado, en los mismos triángulos que miden 12 y 18, si consideramos el segmento que los separa como base, sus alturas serán proporcionales a 12/18 = 2/3, es decir, que si el que mide 12 tiene una altura, por ejemplo, de 8, el otro tendrá una altura de 12, mientras que si en lugar de eso tiene una altura de 14, el otro tendrá una altura de 21.
Pero claro, como el que mide T tiene la misma propiedad respecto al que mide 24, y ambos tienen la mismas alturas, respectivamente, que sus vecinos.
Por lo tanto T/24 también debe ser la fracción 2/3, de forma que T mide exactamente 16.
C) Una vez resuelto el apartado B), es muy sencillo abordar este problema, si tienes la precaución de trazar la diagonal que divide al cuadrilátero en dos triángulos.
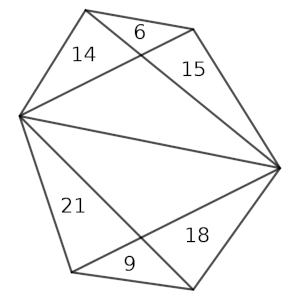
De esta forma, razonando de manera análoga al apartado B), el triángulo superior tendrá un área de 14·15/6 = 35, mientras que el triángulo inferior tendrá un área de 21·18/9 = 42, así que el área del cuadrilátero, que hemos llamado Q en el dibujo, valdrá 35 + 42 = 77.