Problema 2 del nivel B de la Olimpiada Autonómica de la Comunidad Valenciana
Se dirige a una edad de: 14 -15 años

Encuentra todas las funciones polinómicas que son de la forma f(x) = x² + ax + b que cumplen que f(2) = 0 y f(f(3)) = 0.

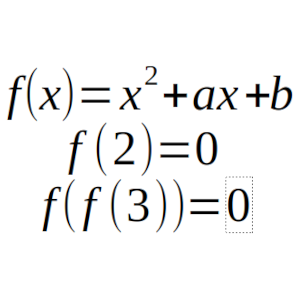
Solución:

Veo dos formas de enfocar el problema.

La primera, si sabemos que f(2) = 0, eso significa que el polinomio x² + ax + c = (x – 2)(x – r) para cierto valor r.

Eso significa que f(3) = (3 – r), ya que 3 – 2 = 1.

Por lo tanto, f(3 – r) = 0, y necesariamente 3 – r = r, por lo que r tiene que valer exactamente 3/2, o bien 3 – r = 2, en cuyo caso r = 1.

Eso quiere decir que hay dos funciones que cumplen las dos cosas simultáneamente, x² – (7/2)x + 3 = (x – 2)(x – 3/2), es decir, que a = -7/2 y b = 3, y x² – 3x + 2 = (x – 2)(x – 1).

La otra forma es, directamente, hacer un sistema, aunque es complicado.

La expresión f(2) = 0 significa que 4 +2a + b = 0, por lo que tenemos la expresión 2a + b = -4, es decir, b = -4 – 2a.

Calcular f(3) es 9 + 3a + b = 5 + a.

f(f(3)) = (5 + a)² + a(5 + a) + b = 25 + 10a + a² + 5a + a³ -4 – 2a = 2a² + 13a + 21, con lo que, resolviendo la ecuación 2a² + 13a + 21 = 0, tendríamos que, o bien a = -3, o bien a = -7/2. En el primer caso, b = 2 y en el segundo b = 3, y por tanto hay dos funciones, x² – 3x + 2 y la función x² – (7/2)x + 3.