Problema 4 del nivel B de la Olimpiada Autonómica de la Comunidad Valenciana Se dirige a una edad de: 14 -15 años
Observa la suma siguiente:
9 + 26 = 35
De los tres números implicados, uno es divisible por 2, pero no todos.
Uno es divisible por 3, pero no todos.
Uno es divisible por 5, pero no todos.
Uno es divisible por 7, pero no todos.
No hay ningún número entero mayor que 1 que divida a los tres números.
Una suma de este tipo, diremos que es interesante.
a) Demuestra brevemente que ningún número mayor que uno divide a dos de los tres números implicados en una suma interesante.
b) ¿Puedes encontrar todas las sumas interesantes en las que el resultado es menor que 30?
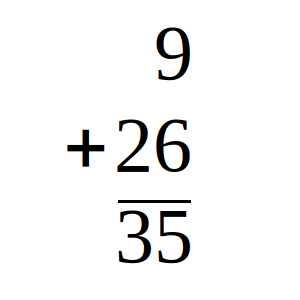
Solución:
Para el apartado a), basta ver que si dos de los tres números son divididos por el mismo factor, entonces el otro también, ya que ap + bp = (a + b)p, y también cp – ap = (c – a)p. Puesto que una suma interesante no puede tener todos sus números divididos por un mismo número mayor que 1, no puede dividir tampoco a dos de ellos.
Para el apartado b), hay que ordenar un poco las posibilidades.
Puesto que uno de ellos debe tener factor 7, y entre 1 y 30 no hay muchos, veremos en qué posición tiene el múltiplo de 7.
Si el resultado es 7, es imposible, ya que al menos otro debe valer 5 y otro 3.
Si el resultado es 14, podríamos tener 5 + 9 = 14, como única opción.
Si el resultado es 21, podríamos tener 15 + 6 = 21, como única opción.
Si el resultado es 28, podríamos tener 25 + 3 = 28 como única opción.
En las demás que encontremos, el número divisible por 7 no es el resultado, así que podemos probar otras variantes.
3 + 7 = 10 es la primera opción con un sumando 7 que cumple todos los requisitos.
5 + 7 = 12 también
8 + 7 = 15 también
15 + 7 = 22 también
18 + 7 = 25 también
20 + 7 = 27 también
Usando el 14, tenemos
1 + 14 = 15
6 + 14 = 20
10 + 14 = 24
Usando el 21, tenemos
4 + 21 = 25
5 + 21 = 26
Y, evidentemente, no podemos usar el 28 como sumando.
En total, tenemos 14 posibilidades.