Problema 0 del concurso Olitele 2022
Se dirige a una edad de: 16-17 años

Hay algunos números de cuatro cifras (es decir, enteros entre el 1000 y el 9999, incluidos) con la siguiente propiedad:

Si hacemos la suma de ellos con 2022 resulta otro número de cuatro cifras y, entonces, si miramos el número resultante, el 2022 y el número de partida, entre todos ellos aparecen los 10 dígitos.

¿Cuánto suman los números que cumplen este enunciado?

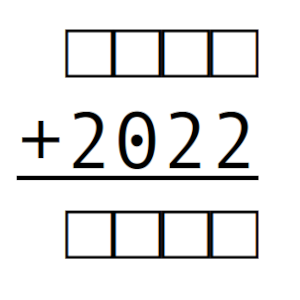
Solución:

La cantidad de trabajo que tenemos este curso, unido a una situación personal más absorbente, ha provocado que se me pasara recomendar la participación en este estupendo concurso.

Es un entretenimiento que puede servir incluso a edades más tempranas.

Es fácil darse cuenta de que en los 8 espacios deben aparecer todos los dígitos entre 0 y 9, excepto el 0 y el 2, así que tienen que aparecer 1, 3, 4, 5, 6, 7, 8 y 9. Por tanto deben aparecer una única vez cada uno de ellos.

Puesto que uno de los dígitos que hay que sumar es el 0, es evidente que los dígitos de las centenas deben sumar más de 10, para que podamos situar en las centenas dígitos diferentes. Un poco más trabajoso es descartar el 7 y el 8 para las centenas, pero eso significa que el 9 y el 1 ocupan obligatoriamente la posición de las decenas, que las centenas serán dos números consecutivos, y que todos los demás dígitos que ocupan las otras dos posiciones se diferencian en 2 unidades.

Por lo tanto, los dígitos 3, 4, 5, 6, 7 y 8 deben situarse de una de cuatro formas:

3 y 4 en las centenas, y 5 y 7 en unidades o unidades de millar y 6 y 8 en la otra posición, o bien 7 y 8 en las centenas y 3 y 5 en las unidades o las unidades de millar y 4 y 6 en la otra posición.

Así, tenemos 4 posibilidades para el número buscado: 5396, 6395, 3794 y 4793.

Rápidamente, podemos comprobar que la suma cumple en cada uno de los cuatro casos el objetivo que tenemos. Y la respuesta es la suma de todos ellos: 20378.