Problema 7 de la Fase Local de la Olimpiada Española de Matemáticas 2023 (sábado) Se dirige a una edad de: 16-17 años
Sea n >= 2 un entero positivo.
Dividimos un rectángulo de n·(n + 1) en piezas rectangulares: dos de 1·1, dos de 1·2, y así sucesivamente hasta dos de 1·n, con la propiedad de que para cada k >= 2, una pieza 1·k tiene los lados largos horizontales y la otra verticales.
Demostrar que, con estas condiciones, las dos piezas 1·1 comparten un lado.
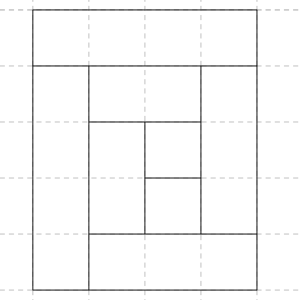
Solución:
En estos casos, es evidente que debemos empezar a trabajar en los casos más simples. Si n = 2, tenemos que dividir un rectángulo 2·3 en cuatro piezas, dos de 1·1, y dos de 1·2, de forma que las dos piezas de 1·2 sean perpendiculares entre sí. Puesto que la pieza 1·2 con el lado largo en vertical ocupa dos filas consecutivas, esta claro que la pieza 1·2 horizontal no puede estar en la fila media, así que o bien se sitúa arriba o bien abajo. De esta forma, la pieza vertical puede ir a la derecha o a la izquierda, pero las dos de tamaño 1 deben estar situadas juntas.
Si n = 3, pasa algo similar con la de tamaño 1·3 horizontal, no puede ocupar más que la primera horizontal o la última, ya que si ocupa una de las intermedias no podremos situar la 1·3 vertical. A su vez, la vertical sólo podremos ponerla en la izquierda o la derecha, ya que en caso contrario no quedaría espacio para situar la 1·2 horizontal, así que una vez que las situemos ambas, nos quedará un rectángulo 2·3 para rellenar, y así lo reducimos al caso anterior.
Esto sugiere que podemos probarlo por inducción. Supongamos probado para un valor n – 1, y veamos que es cierto para el caso n.
La clave está en situar en primer lugar los elementos 1·n, que sólo podremos poner en los extremos, y el rectángulo que queda por cubrir es exactamente (n – 1)·n, que es el que está probado por inducción.
Evidentemente, el horizontal se pone primero, y para poder poner el vertical en algún sitio, debemos situarlo arriba o abajo, quedando libre un cuadrado den tamaño n·n. Después, el vertical hay que ponerlo en el lado izquierdo o el derecho, para poder ubicar más tarde el horizontal 1·(n – 1).