Problema 1 del nivel B de la Fase Comarcal de la Olimpiada de la Comunidad Valenciana
Se dirige a una edad de: 14-15 años

Averigua el valor de x, y, y z en la expresión x² + y² + z² = x – z = 2.

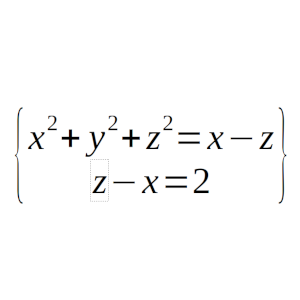
Solución:

Hay una forma de intuir la solución, incluso de demostrar que es correcta.

Observa que x² + y² + z² siempre es un número positivo, de forma que x, y, y z deben estar acotados, ya que suman 2. El mayor valor que pueden tener es raíz de 2, con signo positivo (y el menor, raíz de 2 con signo negativo). Seguro que hay una solución en la que x y z están a la misma distancia del cero, si ambos valen 1 al cuadrado, es decir, que z vale 1 y x vale -1, ya que la diferencia es 2 y la suma de sus cuadrados es 2. En ese caso, y vale 0. es la única solución porque si hubiese una solución en la que y² fuese distinto de cero, eso significaría que x² + z² debería ser menor que 2, y eso es imposible, pues su diferencia es 2, y uno de ellos debe ser positivo y otro negativo, ya que (x – z)² = 4, y x² + z² = 4 + 2xz < 2 implica que 2xz < -2, es decir, que xz < -1. Pero z = x + 2, por lo que x² + 2x < -1 y por tanto x² + 2x + 1 < 0 , y (x + 1)² = x² + 2x + 1 siempre es positivo.

Otra forma de llegar a la misma conclusión es más algebraica. Sustituyendo z por x + 2 en la primera igualdad. Llegamos a que x² + y² + (x + 2)² = (x + 2) – x.

De esta forma, tenemos, quitando paréntesis, que x² + y² + x² + 4x + 4 = x + 2 – x, lo que nos lleva a la ecuación 2x² + 4x + 2 + y² = 0.
Si vemos esto como una ecuación de segundo grado en x, en la que el coeficiente de x² es 2, el coeficiente de x es 4 y el término independiente es 2 + y², entonces, aplicando la fórmula, tenemos que x = (- 4 +- raíz (16 – 4·2·(2 + y²)))/4 = (-4 +- raíz(16 – 16 – 8y²))/4 = (-4 +-raíz(-8y²))/4.

Pero para poder calcular x, necesitamos que la raíz cuadrada se calcule sobre un número no negativo, y -8y² por tanto debe ser 0, es decir, la única solución posible para y es que sea 0. En ese caso, x = -4/4 = -1, y por tanto z = 1. Sólo tenemos, por tanto, esa solución, (-1, 0, 1).