Problema 2 del primer nivel de la Olimpiada de Mayo 2023
Se dirige a una edad de: 11-12 años

Decimos que un número de cuatro dígitos abcd es cabuloso si el número a⁴ + b³ + c² + d es igual al número de dos dígitos cd.

Por ejemplo, 2023 es cabuloso, pues 2⁴ + 0³ + 2² + 3 = 23.

¿Cuántos números cabulosos hay?

Aclaración. a⁴ es el resultado de multiplicar 4 veces el número a, por ejemplo, 3⁴ = 3·3·3·3 = 81.

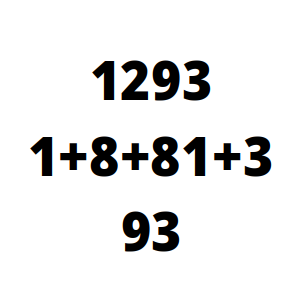
Solución:

La potencia más alta es la primera cifra elevada a 4, que sólo puede ser un número entre 1 y 3, ya que 4⁴ = 256, y tiene ya 3 cifras.

La expresión habitual de los últimos dos dígitos es 10c + d

Si tratásemos de encontrar un número cabuloso que empezase por 1, nos debemos centrar en que 1 + b³ + c² + d = 10c + d, es decir, que 1 + b³ + c² = 10c, 1 + b³ = (10 – c) c. Es suficiente probar los números enteros c posibles, en los que (10 – c)c puede dar, respectivamente, 0, 9, 16, 21, 24, 25 y los mismos valores para los siguientes dígitos, 24, 21, 16 y 9. De todos ellos, sólo 9 da un cubo al restarle 1, por lo que los posibles valores serían
1210, 1211, 1212, 1213, 1214, 1215, 1216, 1217, 1218 y 1219, pero también 1290 y los 9 siguientes.

En segundo lugar, buscar un número cabuloso que empiece por 2, tendríamos que 16 + b³ + c² + d = 10c + d, por lo que de nuevo tendríamos b³ = (10 – c)c – 16. Puesto que no puede ser negativo, tendremos que estudiar sólo los valores en los que la expresión (10 – c)c – 16 es positiva, pero los únicos valores mayores que 16 son 16, 21, 24 y 25, y las diferencias con 16 serían 0, 5, 8 y 9, con lo que los únicos cubos serían 0 y 8, con lo que tendríamos los números 2020 y los 9 siguientes, 2240 y los 9 siguientes, 2260 y los 9 siguientes y 2080 y los 9 siguientes.

Pero no hay ningún número cabuloso que empiece por 3, ya que en ese caso, debería cumplirse que 81 + b³ + c² + d = 10c + d, por lo que b³ = (10 – c)c – 81, y la expresión (10 – c)c no puede alcanzar valores superiores a 25.

Por tanto serían esos todos los números posibles, un total de 60.