Problema 3 del primer nivel de la Olimpiada de Mayo 2023 Se dirige a una edad de: 11-12 años
Sobre una recta l hay cuatro puntos, A, B, C y D en ese orden, tales que AB = BC = CD.
Se elige un punto E fuera de la recta l de modo que al trazar los segmentos EB y EC se forme un triángulo equilátero EBC.
A continuación se trazan los segmentos EA y ED y se elige un punto F de modo que al trazar los segmentos FA y FE se forme un triángulo equilátero FAE exterior al triángulo EAD.
Por último se trazan las rectas EB y FA, que se cortan en el punto G.
Si el área del triángulo EBD es 10, calcula el área del triángulo EFG.
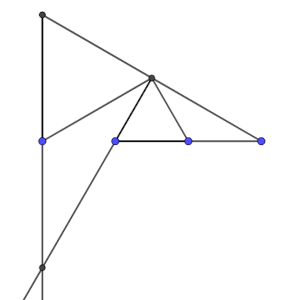
Solución: Aquí.