Problema 3 del primer nivel de la Olimpiada de Mayo 2023 Se dirige a una edad de: 11-12 años
Sobre una recta l hay cuatro puntos, A, B, C y D en ese orden, tales que AB = BC = CD.
Se elige un punto E fuera de la recta l de modo que al trazar los segmentos EB y EC se forme un triángulo equilátero EBC.
A continuación se trazan los segmentos EA y ED y se elige un punto F de modo que al trazar los segmentos FA y FE se forme un triángulo equilátero FAE exterior al triángulo EAD.
Por último se trazan las rectas EB y FA, que se cortan en el punto G.
Si el área del triángulo EBD es 10, calcula el área del triángulo EFG.
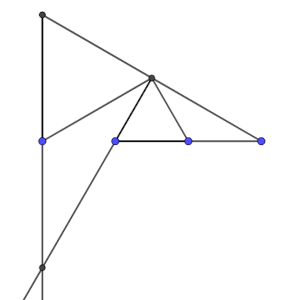
Solución:
Lo más difícil es hacer el dibujo siguiendo las instrucciones. Aquí tenemos el dibujo, y observamos que se puede intuir que el triángulo EBD y el EFG son semejantes, de forma que es posible, encontrando la razón de semejanza, calcular el área de uno conociendo la del otro.
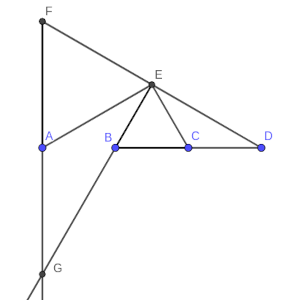
En primer lugar hay que mostrar que en efecto son semejantes, y después calcular la proporción.
Antes de su semejanza, podemos apreciar que EBD parece un triángulo rectángulo, pero ¿lo es realmente?
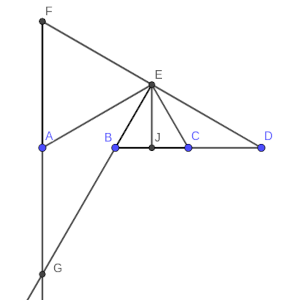
Una manera en que yo lo veo es hacer la construcción con una medida concreta, y comprobar que EBD cumple el Teorema de Pitágoras. Por eso es rectángulo.
Si añadimos el punto medio entre B y C, que le he llamado J, y elegimos la distancia entre A y B como 2 unidades, la distancia entre B y J es 1, y la distancia entre B y E, por construcción es 2, así que la distancia entre E y J es la raíz cuadrada de 3, y es perpendicular EJ a la recta l.
Aplicando el Teorema de Pitágoras, los catetos miden 3 y raíz de 3, así que la distancia entre E y D es de raíz de 12.
Ahora que tenemos los tres lados, EB = 2, BD = 4 y ED = raíz de 12, comprobamos que 12 + 2² = 4², es decir, que efectivamente es un triángulo rectángulo.
Claramente el ángulo recto BED se divide en 3 ángulos de 30 grados (los dos que forman el triángulo equilátero y la diferencia.
Por simetría, el ángulo BEA también mide 30, y al añadirle el triángulo equilátero AEF, vemos que también es rectángulo el triángulo EFG, y también tiene un ángulo agudo de 60 grados.
En cuanto a la proporción, vemos que el segmento EB debe ser proporcional al segmento EF. En lo que hemos calculado, EB mide 2 unidades, y EB mide lo mismo que EA y ED, raíz de 12.
Por lo tanto la proporción será de raíz de 12 partido por 2, que es raíz de 3, por lo que el área será 3 veces más grande (tanto la base como la altura se multiplicarán por este factor raíz de 3), así que el área real de EFG será 3·10 = 30.