Problema 2 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
El abuelo, la abuela y Pau comen juntos un domingo.
Para postre, el abuelo ha comprado tres brazos de gitano, uno de nata, uno de trufa y uno de crema.
Pau dice: “Abuelo, para repartirlos mejor, podrías partir cada uno en tres trozos exactamente iguales”. Y así lo hace el abuelo.
Entonces, Pau pregunta: “¿De cuántas formas nos los podemos repartir si cada uno debe escoger tres trozos?
El abuelo no supo responderle a la pregunta en ese momento.
¿Qué respuesta darías tú?
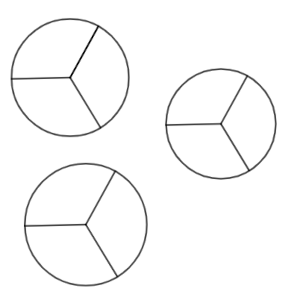
Solución:
Se trata de un problema de recuento, en el que podemos aplicar combinatoria si tenemos recursos, pero también contar a mano, si tenemos un poco de paciencia.
Si llamamos A, B y C a cada uno de los sabores, y ponemos un número a cada uno de los trozos que tocan a cada uno, podemos indicar un reparto poniendo el código que le toca al abuelo, la abuela y a Pau, en ese orden.
Probando los tres sabores, tenemos el único reparto
A1B1C1, A1B1C1, A1B1C1
Si el uno de ellos toma dos de un tipo y uno de otro, puede ocurrir que los otros dos hagan lo mismo:
A1B2, B1C2, C1A2, que podría ocurrir de 6 formas diferentes si cambiamos la situación de los comensales, y otras 6 si hacemos un cambio en la mezcla de sabores (A1C2, C1B2, B1A2) (12 repartos en total).
Hay dos posibilidades más, una es que otro tome de los tres tipos:
A1B2, B1A1C1, A1C2, que de nuevo se multiplica por 6 cambiando posición.
Ahora bien, habrá 3 posibles situaciones según qué sabor es el que toman las tres personas (18 repartos en total).
Y una última posibilidad, que otro sólo tome un tipo de sabor, con lo que tendremos:
A1B2, C3, A2B1, que de nuevo marcará 12 repartos diferentes, según qué sabor sólo pruebe uno de ellos y cómo se haga el reparto.
Por último, hay 6 repartos en los que cada uno sólo prueba un sabor:
A3, B3, C3.
En total, hay 6 + 12 + 18 + 12 + 1 = 49 posibles repartos en total.