Problema 3 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
Los puntos E, F, G y H son puntos del lado del cuadrado ABCD que cumplen AE = BF = CG = DH y, además, AE = n·EB, donde n es un valor real positivo.
¿Qué fracción del área del cuadrado ABCD representa el área del triángulo sombreado?
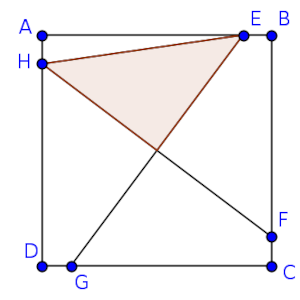
Solución:
Hay varias maneras de abordar esto, pero la idea que me parece más sencilla es tratar de calcular el área de ese fragmento y el área de todo el cuadrado, para luego calcular la fracción.
En nuestro caso, como hay que hacerlo en función de n (a los participantes se les daba un valor de n diferente a cada uno), lo mejor es hacer que el segmento EB valga 1 (la unidad de medida lineal), y así AE mide n y AB mide (n + 1), es decir, que el área del cuadrado será (n + 1)² o, si prefieres los polinomios, n² + 2n + 1.
Ahora bien, ¿Cómo calculamos el área de ese triángulo?
A mí se me ocurre buscar simetrías, y ver que el triángulo está dividido en cuatro zonas que son cuadriláteros iguales, y la zona en la que está ese triángulo está dividida en dos triángulos, el que nos ocupa y otro rectángulo, el AEH.
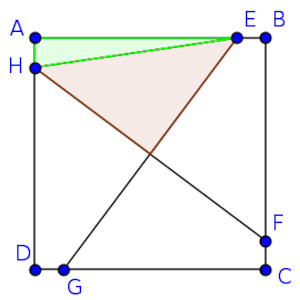
Entonces, el área del cuadrilátero sería (n + 1)²/4, y como el área de AEH es el área de un triángulo rectángulo, es muy fácil ver que es el producto de sus catetos, n/2.
Resumiendo, el área de la zona sombreada originalmente será (n + 1)²/4 – n/2. Para ponerlo en una misma fracción, sería (n² + 2n + 1)/4 – 2n/4 = (n² + 1)/4.
Y por tanto, el cociente que buscamos será el resultado de dividir ambos números (en nuestro caso, expresiones polinómicas): (n² + 1)/(4n² + 8n + 4), que por lo general no se puede simplificar.