Problema 4 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
Antes de probar con este problema, deberíamos saber que el factorial de un número natural n, que se escribe n!, es n! = 1·2·3·…·(n – 1)·n.
Consideremos el número P, que se consigue de la siguiente manera: P = 1!·2!·3!·…·98!·99!·100! (es decir, como el producto del factorial de los 100 primeros números).
¿Cuál es el valor del número natural s para el cual Q = P/(s!) es un cuadrado perfecto de un número natural?
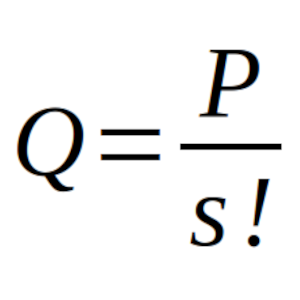
Solución:
La clave en este problema es probar lo que sucede con valores más pequeños, principalmente pares, y generalizar. Yo me centré muy pronto en estudiar si tenía el resultado una cantidad par o impar de factores primos (si tiene una cantidad par es un cuadrado perfecto, y si no, no).
Imaginemos que estamos buscando cómo es el número 1!·2!·3!·4!·5!·6!.
Si contamos cuántos factores 5 tiene, tiene 2, sin embargo, tiene 7 factores 3 y 12 factores 2. Está claro que no es un cuadrado perfecto. Evidentemente no tiene primos mayores.
Si buscamos qué factorial habría que quitar para que fuese un cuadrado perfecto, Deberíamos quitar algún factor 3, por ejemplo podríamos tratar de hacerlo con el factorial de 3, de 4 o de 5 (el de 6 no nos conviene, ya que tiene dos factores 3, y seguiría teniendo una cantidad impar).
Sin embargo, no nos interesa quitar ningún factor 5, por lo que nos quedamos con 3 o con 4. Pero ambos factoriales tienen una cantidad impar de factores 2, así que no existe ningún factorial que al dividir por él nos dé un cuadrado perfecto.
Probemos con 8 factoriales, se trataría del número 1!·2!·3!·4!·5!·6!·7!·8!.
Este número sí tendría dos factores 7, 4 factores 5, 9 factores 3 y nada menos que 23 factores 2. De nuevo debemos quitar al menos un factor 3 sin quitar ningún 5, volviendo al 3 o al 4, y ambos satisfacen la propiedad de quitar también una cantidad impar de doses.
La idea es trabajar este método para un número tan grande como el que tenemos en el problema.
Si consideramos los primos mayores que 50, tendremos que, por ser primos impares, aparecen una única vez en cada factorial a partir de su número correspondiente, aportando una cantidad par de factores a la factorización. Por tanto no debemos dividir por un número mayor de 53.
Sin embargo, el 47 aparece una cantidad impar de veces, por lo que deberemos quitarlo exactamente una vez. Eso limita el valor de s a 47, 48, 49, 50, 51, o 52.
El 7 juega ahora un papel importante, habrá que crear una estrategia de recuento y ver cuántas veces nos conviene extraerlo. El 7 aparece 1 vez entre 7 y 13, 2 veces a partir de 14 hasta 20, y así sucesivamente. Podemos pensar que es 7·(1 + 2 + 3 + 4 +…+ 13) hasta el 97, y luego añadir 14·3, pero nos olvidaríamos entonces del factor extra que aparece a partir del 49, y otro más a partir del 98 (que es el doble de 49), lo que haría un total de 49 + 2·3. En total, por tanto, sale un número par de factores 7, de manera que debemos quitar un número entre 49 y 52.
Afinando poco a poco con todos los factores primos, llegué a la conclusión de que debe tratarse exclusivamente del valor 50, ya que es el único factorial que tiene una cantidad adecuada de factores de cada primo. Sin embargo, es complicado hacer un conteo exhaustivo por este método de todos los factores primos del número.
La idea alternativa para ver que funciona, es pensar que cada factorial se puede transformar en el anterior si le quitamos el último número, de forma que n!·(n + 1)! = (n!)²·(n + 1).
Si procedemos a quitar justo los pares hasta 100, tendríamos 1!²·3!²·…·99!²·2·4·6·…·98·100 = 1!²·3!²·…·99!²·50!·2⁵⁰. Evidentemente, si quitamos el factorial de 50, se trata de un cuadrado perfecto.
Claro, que esto no prueba que si quitas algún otro factorial no tengas también un cuadrado perfecto, para eso sería necesario bajar a ver los factores individuales.