Problema 5 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
Se considera un dibujo con algunas circunferencias concéntricas y algunas rectas paralelas, y miramos el número de intersecciones entre rectas y circunferencias, el plano queda descompuesto en algunas regiones según las posiciones relativas que tengan.
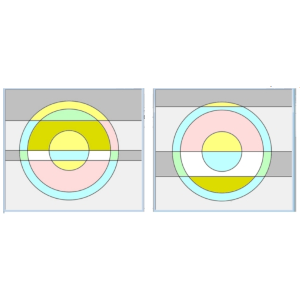
La imagen muestra un par de situaciones con tres rectas y tres circunferencias: En la primera, el plano queda dividido en 20 regiones y en la segunda en 16.
¿Cuál es el máximo número de regiones en que queda descompuesto el plano por c circunferencias concéntricas y r rectas paralelas?
Solución:
Viendo las imágenes, es sencillo darse cuenta que cada circunferencia, dibujada antes de las líneas, aporta una nueva región al plano, así que una vez dibujadas las c circunferencias, el plano queda dividido en c + 1 regiones.
Ahora, el número de regiones en las que cada nueva línea divide la plano no es siempre al mismo.
El máximo se alcanza cuando es mayor el número de intersecciones, y por tanto para alcanzarlo es necesario que todas las rectas corten a la circunferencia central.
La primera recta añadirá c + 1 regiones, porque cortará a todas las circunferencias y separará al plano central, pero las regiones en todas las circunferencias están conectadas. Sin embargo, todas las demás líneas generarán 2c + 1 regiones, ya que las nuevas zonas, tanto en el plano como en las circunferencias, estarán divididas en dos partes, excepto en la circunferencia central.
Por tanto, el número máximo de regiones será 2c + 2 + (r – 1)(2c + 1) = 2rc + r + 1.

En el caso del dibujo que tenemos de referencia se puede llegar a dividir en 22 regiones si todas las rectas cortan a la circunferencia central.