Problema 7 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
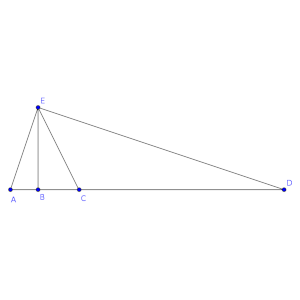
En el triángulo rectángulo AED de la figura, rectángulo en E, AB es la altura sobre la hipotenusa y EC es la bisectriz del ángulo recto.
Si se cumple que la razón de distancias entre AC y CD es 1:3, razona cuál es la proporción entre las distancias de los tres segmentos AB, BC y CD en que ha quedado dividida la hipotenusa.
Nota: seguramente no es la única manera de enfocar el problema, pero puede ser interesante que se comience por calcular la relación de distancias AB:BD.
Solución:
No he hecho mucho caso a la sugerencia, y seguramente hay formas de enfocarlo mejor, pero voy a dar mi respuesta.
Lo que he hecho es situar unas medidas concretas, una unidad en AC y tres unidades en CD. A partir de ahí, tratar de calcular el valor de AB.
Puesto que el segmento EC es bisectriz, divide el ángulo de 90º en dos de 45º.
Al ser un triángulo rectángulo, podemos poner que AE² + ED² = 16, ya que AD mide AC + CD.
En el triángulo AEC, tenemos un ángulo y un lado, podemos aplicar el teorema de los senos, ya que tenemos el seno del ángulo ECA, 45º, cuyo seno es raíz(2)/2, y el seno del ángulo CAE, que pertenece al triángulo rectángulo, por lo que es ED/4. El lado AC mide cuatro, por lo que tenemos que raíz(2)/2 = ED/(4EC).
Aplicando algo similar en el triángulo ECD, tendremos que raíz(2)/6 = AE/(4EC).
Con esto, podemos poner AE y ED ambos en función de EC, ya que de la primera igualdad tendremos que ED = 2raiz(2)EC, mientras que de la segunda tendremos que AE = 2raíz(2)EC/3.
Puesto que la relación que combina AE y ED los expresa al cuadrado, vamos a elevar al cuadrado estas relaciones, obteniendo que ED² = 8EC², y que AE² = 8EC²/9.
Por tanto 8EC² + 8EC²/9 = 16, por lo que EC² + EC²/9 = 2, y por tanto 9EC² + EC² = 18. De todo esto deducimos que EC² = 18/10 = 9/5.
Así, tenemos que EC = 3/raíz(5) = 3raíz(5)/5. Por tanto, AE = 2raíz(10)/5 y ED = 6raíz(10)/5.
Usando los tres lados del triángulo rectángulo, podemos tener todas las razones trigonométricas de los dos ángulos del triángulo rectángulo AED, y como coincide con uno del triángulo AEB, vemos que AB = cos(BAE)·AE = (AE/4)·AE = AE²/4 = 40/100 = 4/10 =0,4 y, claro, BC = 1 – 0,4 = 0,6.
Puesto que las proporciones suelen representarse con números enteros, representaremos la proporción 0,4;0,6:3 multiplicada por 5 (que es equivalente a que hubiésemos tomado tamaños 5 veces mayores en el trabajo inicial), como 2:3:15 como proporción entre AB, BC y CD.