Problema 9 del concurso Olitele 2022
Se dirige a una edad de: 16-17 años

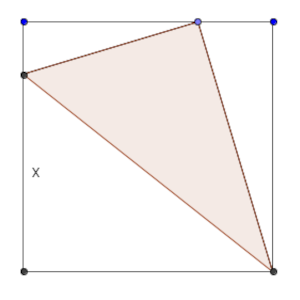
Queremos descomponer un cuadrado de 1 metro de lado en cuatro triángulos rectángulos como los indicados en la figura.

Encuentra el menor valor de x para el que es eso posible, y calcula, en caso de ser x el valor mínimo, qué área tendrá el triángulo rectángulo coloreado.

Solución:

Hay que darle unas pocas vueltas, hasta que nos damos cuenta de que dos de los triángulos son semejantes, los que coinciden con el ángulo recto del que está coloreado, puesto que sus dos ángulos deben sumar 90º porque al añadirse al ángulo recto del coloreado dan 180º.

Entonces, si llamamos z al cateto pequeño del mayor de ellos, el cateto grande de ese mide 1, y el cateto grande del otro mide 1 – z, por lo que el cateto más pequeño del triángulo más pequeño, por ser proporcional, medirá z(1 – z) = z – z².

Eso quiere decir que x = 1 – (z – z²), es decir, que x = z² – z + 1.

Por lo tanto, el valor de x dibuja una parábola para los posibles valores de z entre 0 y 1. Y su vértice está claro por la fórmula que tiene que está en ½ = 0,5, así que el menor valor posible de x se dará para el caso en que z vale ½, y x valdrá en ese caso ¼ – ½ + 1 = ¾ de metro, 75 centímetros.

El valor del área para x = ¾, será, restándole al área del cuadrado los tres triángulos cuyos lados perpendiculares son más sencillos de calcular, 1 – ⅜ – 1/16 – ¼ = 5/16 de metro cuadrado, 3125 centímetros cuadrados. También es posible calcular los dos catetos del triángulo rectángulo coloreado utilizando el Teorema de Pitágoras, pero no es necesario.