Problema 10 del concurso Olitele 2022 Se dirige a una edad de: 16-17 años
Si a, b y c son tres números reales diferentes de cero que cumplen la siguiente igualdad:
(a + b)/c = (b + c)/a = (c + a)/b = R
¿Qué valor o valores reales puede tener R?
Si para un cierto valor de K (número real diferente de cero) existen tres números reales diferentes de cero a, b y c tales que
(a + Kb)/c = (b + Kc)/a = (c + Ka)/b = S
¿Para qué valores de K resulta que S puede tener un único valor?
¿Cuál es ese valor de S (y cómo depende de K)?
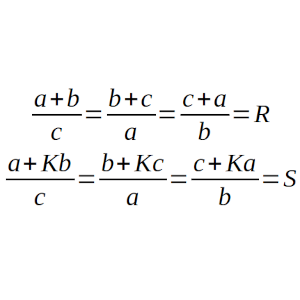
Solución:
Vayamos por el primer apartado.
De la colección de igualdades, tenemos que (a + b)/c = R, de forma que a + b = Rc. De la misma forma, tenemos que b + c = Ra, y que c + a = Rb.
Por lo tanto, se debería dar la igualdad si sumamos las tres igualdades, y al ser tan simétricas, tendríamos que 2a + 2b + 2c = R(a + b + c).
Eso quiere decir que o bien (a + b + c) vale 0, o bien R = 2.
Si R = 2, tenemos que a + b = 2c, por lo que a = 2c – b. Sin embargo, entonces c + b = 2a = 4c – 2b, pero en ese caso tenemos que 3b = 3c, por lo que b = c, y además a = 2c – c = c, por lo que a, b y c son iguales.
Por lo tanto tenemos que a + b + c = 0. Eso quiere decir que a + b = -c y por tanto R debe valer -1, ya que (a + b) /c = -1 (y las otras fracciones son iguales).
En definitiva, R vale -1, o bien R = 2 ( en el caso en que sean todos iguales).
Tomemos ahora el segundo apartado.
Claramente, K no vale 1, porque en ese caso S puede tener dos valores.
Sin embargo, suponiendo que la K no vale 1, llegaremos a que S debe valer K + 1, y encontraremos unos valores en los que esto suceda.
De manera análoga, tenemos que a + Kb = Sc, b + Kc = Sa, y c + Ka = Sb, por lo que (a + b + c) + K(a + b + c) = S(a + b + c). Si a + b + c no vale 0, claramente S = 1 + K.
¿Qué sucede si a + b + c = 0? Pues no se puede dar la igualdad, ya que a + Kb = a + b + (K – 1)b, por lo que (a + Kb)/c = (-c + (K – 1)b)/c = -1 + (K – 1)b/c = S. Debido a esto, (K – 1)b/c = S + 1.
De manera análoga, en este caso, tenemos que (K – 1)c/a = S + 1 y (K – 1)a/b = S + 1.
Puesto que K no vale 1, tenemos que b/c = c/a = a/b, pero en ese caso los tres deberían tener el mismo signo, por lo que es imposible que a + b + c = 0.
Bien, entonces supongamos que tenemos que a + Kb = (K + 1)c. ¿Qué valores podríamos usar para a, b y c? Claramente, deben ser iguales, por ejemplo, a = 1, b = 1 y c= 1.
Así que K distinto de 1, y S debe ser K + 1 ( y los tres números son iguales).