Problema 1 del nivel A de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 12 -13 años
Sabiendo que a + b = 3 y que a² + b² = 29, ¿Cuál es el valor de a³ + b³?
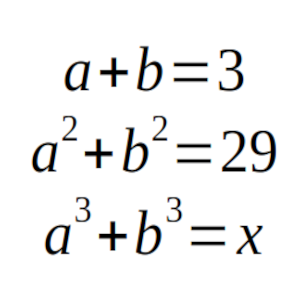
Solución:
Para resolver este problema, es necesario conocer la propiedad algebraica llamada distributiva, que nos permite multiplicar un par de sumas, y sacar, si es necesario, factor común.
¿Cómo conseguimos a³ + b³ a partir de a² + b²? Si multiplicamos (a² + b²)(a + b) = a³ + a²b + b²a + b³ = a³ + b³ + a²b + b²a = a³ + b³ + ab(a + b). Es necesario por tanto obtener ab.
Sin embargo, si tenemos en cuenta que (a + b)(a + b) = a² + ab + ba + b² = a² + b² + 2ab, es posible obtener ab a partir de lo que tenemos, ya que 3·3 = 29 + 2ab, por lo que 2ab = -20, es decir, ab = -10.
Y por tanto, como hemos puesto anteriormente, 29·3 = a³ + b³ +(-10)·3, por lo que 87 + 30 = a³ + b³, es decir, que lo que buscamos es que a³ + b³ = 117.
Es evidente que otra solución sería resolver el sistema que nos dan para averiguar el valor de a y de b, elevarlos al cubo y sumarlos, ya que la solución es que o bien a = -2 y b = 5, o bien a = 5 y b = -2. En ambos casos tenemos las dos igualdades y es sencillo ver que a³ + b³ = 117.