Problema 1 del nivel B de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 14 -15 años
En el rectángulo ABCD, de lados AB = 4 cm, y BC = 5 cm, se ha inscrito el cuadrilátero A’B’C’D’, haciendo que AA’ = BB’ = CC’ = DD’ = x.
Escribe la función que expresa el área de A’B’C’D’ en función de x.
¿Cuál es el dominio de la función?
¿Para qué valor de x se alcanza el mínimo?
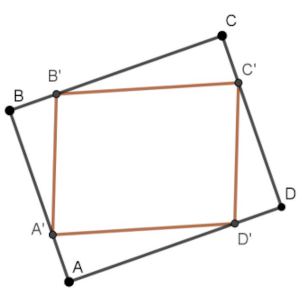
Solución:
Para un valor concreto de x, podemos encontrar el área del cuadrilátero restando a la del rectángulo los cuatro triángulos rectángulos, que son la diferencia entre ambos.
Hay dos tipos de triángulos, los BB’A’ y C’DD’ tienen la misma área, de hecho forman un rectángulo.
Los otros dos también forman un rectángulo.
Las áreas de estos dos rectángulos serían el producto de sus lados.
x(4 – x) = 4x – x²
x(5 – x) = 5x – x²
Al restárselo a 12, que es el área del rectángulo inicial, tendremos la función polinómica:
A(x) = 20 – 9x + 2x²
Si has visto algo de funciones, sabrás que se trata de una parábola.
El dominio es cuando tiene sentido tomar valores de x, es decir, entre 0 y 4, ya que el lado más corto mide 4 y no tiene sentido tomar valores mayores de x. Así que el dominio es el intervalo (0, 4).
El valor mínimo se alcanza en el vértice, para el valor de la x que coincide con –b/(2a), donde b es el coeficiente de la x y a el de la x². Por tanto, sería +9/4 = 2.25, donde se alcanzaría el cuadrilátero de área menor posible.
Otra forma de verlo (más compleja) es cuadrarlo, es decir, convertirlo en el cuadrado de una suma, más un número. De esta forma
20 – 9x + 2x² = (40 – 18x + 4x²)/2 = (40 – 2·(9/2)·(2x) + (2x)²)/2 = (79/4 + (9/2)² – 2·(9/2)·(2x) + (2x)²)/2 = (79/4 + (9/2 – 2x)²)/2
Y, claro, visto como una suma, está claro que el resultado menor posible es cuando el sumando al cuadrado da cero, ya que siempre es positivo. Y eso sólo sucede cuando x = 9/4.