Problema 3 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sea ABCD un cuadrilátero.
Sean J e I los puntos medios de las diagonales AC y BD, respectivamente.
Sea G el punto de la recta BC tal que DG es perpendicular a BC y sea H el punto de la recta AD tal que CH es perpendicular a AD.
Las rectas DG y CH se cortan en el punto K.
Sea E el punto de la recta BC tal que AE es perpendicular a BC y sea F el punto de la recta AD tal que BF es perpendicular a AD.
Las rectas AE y BF se cortan en el punto L.
Probar que KL es perpendicular a JI.
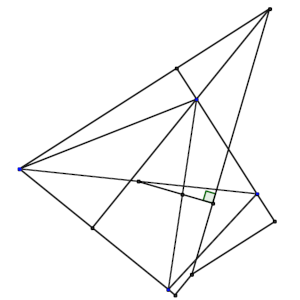
Solución:
La solución oficial utiliza algunos recursos que no todos los estudiantes tienen.
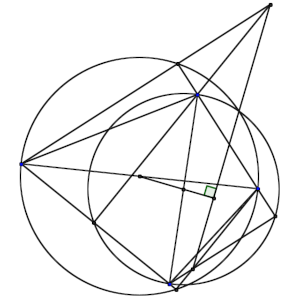
La idea clave en la solución oficial es utilizar los puntos medios de las diagonales para construir círculos que pasan por los dos extremos.
En ese caso, las diagonales se convierten en diámetros de cada una de las circunferencias, y, como se forma un ángulo recto que utiliza esos extremos, los puntos H y E pertenecen a una circunferencia, y los puntos G y F pertenecen a otra.
Ahora, hay una semejanza clara en los triángulos rectángulos HKD y KGC, por lo que el punto K tendrá la misma potencia respecto a las dos circunferencias, y de forma similar con LEB y LFA, por o que L también.
Los puntos que tienen la misma potencia están sobre una recta perpendicular a la que une los centros, por lo que tendremos como consecuencia la perpendicularidad.
La pega que le veo es que necesitas tener claros los conceptos de potencia (la semejanza entiendo que es posible verla), y saber qué es el eje radical, el conjunto de puntos que tiene la misma potencia, y que es perpendicular a la que une los centros.
Voy a tratar de construir una demostración que use sólo vectores y rectas, y elementos de geometría algebraica.
Como lo que tengo que probar es que dos segmentos son perpendiculares, voy a poner uno de los ejes sobre uno de los segmentos.
Concretamente, el eje X va a ser el que contiene los puntos J e I, ya que son los más sencillos de construir. Usaré J como centro, y el punto I va a ser (h, 0) para algún valor h (positivo o negativo).
Eso quiere decir que las diagonales están construidas cada una de ellas sobre dos vectores opuestos.
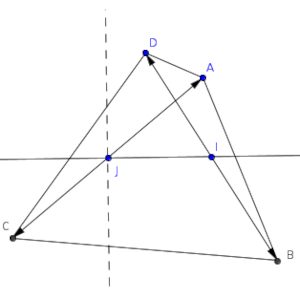
Ahora, vamos a usar coordenadas para los diferentes puntos. A será el punto (a, b), B será el punto (h + c, -d), C será el punto (-a, -b) y D será el (h – c, d). Observo que en realidad los números a, b, c y d podrían ser positivos o negativos, según la posición relativa de los diferentes vértices del cuadrilátero, pero eso no va a afectar a los cálculos posteriores.
El vector BC será (h + c + a, b – d), así que las rectas perpendiculares a BC serían de la forma (h + c + a)x + (b – d)y = k para algún k. En particular, si pasan por A, la k debe valer (h + c + a)a + (b – d)b = a² + ah + ac + b² – bd.
El vector DA será (h – c – a, d – b), así que las rectas perpendiculares a AD serán de la forma (h – c – a)x + (d – b)y = k para algún valor de k. Al pasar por B, la k debe valer (h – c – a)(h + c) + (d – b)(-d) = h² + hc – ch – c² – ah – ac – d² + bd = h² – c² – ah – ac – d² + bd.
Ahora, hay que ver dónde se cortan las rectas de ecuaciones siguientes, el punto K:
(a + h + c)x + (b – d)y = a² + ah + ac + b² – bd
(h – c – a)x + (d – b)y = h² – c² – ah – ac – d² + bd
En particular, queremos obtener la x, ya que del punto de corte, K, queremos estar seguros de que pasa una perpendicular al eje x, así que necesitamos su coordenada x, para ver si es igual o no que la del punto L.
Puesto que observamos que la y tiene el mismo coeficiente, es muy sencillo eliminarlo por reducción sumando, de forma que queda la siguiente ecuación:
2hx = a² + b² – c² – d² + h²
Por lo que x = (a² + b² – c² – d² + h²)/(2h) en el punto K. Si repetimos el proceso para L debe dar lo mismo. Veamos.
El vector BC será (h + c + a, b – d), así que las rectas perpendiculares a BC serían de la forma (h + c + a)x + (b – d)y = k para algún k. En particular, si pasan por D, la k debe valer (h + c + a)(h – c) + (b – d)d = h² – ch + ch – c² + ah – ac + bd – d² = h² – c² + ah – ac + bd – d².
El vector DA será (h – c – a, d – b), así que las rectas perpendiculares a AD serán de la forma (h – c – a)x + (d – b)y = k para algún valor de k. Al pasar por C, la k debe valer (h – c – a)(-a) + (d – b)(-b) = -ah + ac + a² – db + b².
Ahora, hay que ver dónde se cortan las rectas de ecuaciones siguientes, el punto L:
(a + h + c)x + (b – d)y = h² – c² + ah – ac + bd – d²
(h – c – a)x + (d – b)y = -ah + ac + a² – db + b²
En particular, queremos obtener la x del punto de corte, L
Puesto que observamos que la y tiene el mismo coeficiente, es muy sencillo eliminarlo por reducción sumando, de forma que queda la siguiente ecuación:
2hx = a² + b² – c² – d² + h²
Por lo que x = (a² + b² – c² – d² + h²)/(2h) en el punto L.
Por tanto, K y L están sobre una recta perpendicular al eje. Y con eso queda finalizada la demostración.