Problema 2 del nivel B de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2024
Se dirige a una edad de: 14 -15 años

Demuestra que las dos bisectrices externas tA y tB en los puntos A y B concurren formando un ángulo que es la media aritmética de α y β.

Nota: una bisectriz externa tA por A es aquella recta que forma el mismo ángulo δ exterior al triángulo con b y con c. Observa la figura:

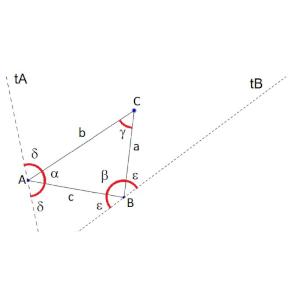
Solución:

Hubo dos preguntas muy repetidas en este ejercicio, qué significaba concurren, que era que se cortan al prolongarlas, y qué era la media aritmética, de la que lo único que revelamos era que era la “media habitual”.

La esencia era completar triángulos, ya que está claro que se cortan. Empezamos por observar que tanto α como β son ángulos menores que 180º por estar en un triángulo, y el ángulo que forman las bisectrices externas con los lados del triángulo es el mismo por los dos lados y suma 180º con el ángulo del triángulo, como se aprecia en la figura. Con eso tenemos dos igualdades: 2δ + α = 180 y 2ε + β = 180. Además, el ángulo x donde concurren las dos bisectrices forma un triángulo con δ y con ε, por lo que δ + ε + x = 180. Ahora se puede trabajar en este sistema, por reducción o por sustitución, para eliminar las variables δ y ε, y se comprueba el enunciado: Por ejemplo, multiplicando por 2 la tercera ecuación, tenemos que 2δ + 2ε + 2x = 360, y si le restamos la primera de las ecuaciones para eliminar δ, tenemos que 2ε + 2x – α = 180, y si restamos la segunda para eliminar ε, tenemos que 2x – α – β = 0. Despejando ahora la x, tenemos que 2x = α + β, por lo que x = (α + β)/2, que es la fórmula de la media aritmética.

También se puede jugar con un valor concreto y ver que se cumple, y observar que si modificas uno de los dos ángulos, la media se modifica la mitad de la modificación, y lo mismo pasa con el ángulo, pero es necesario mantener el dibujo del triángulo que forma el lado del triángulo original y las dos bisectrices externas, el hecho de que sumen 180º esos tres ángulos es fundamental.