Problema 4 del concurso Marató de problemes 2024
Se dirige a una edad de: 14-15 años

Un recipiente está formado por un cilindro y un cono unidos, con una altura total de 50 cm, y contiene cierto líquido.

Cuando el recipiente está en posición vertical y el cilindro está en la parte inferior, el líquido llega a una altura de 22 cm.

Sin embargo, si se coloca con el cono en la parte inferior, el líquido alcanza una altura de 39 cm.

¿Qué parte del recipiente (expresado como fracción irreducible) ocupa el líquido que contiene?

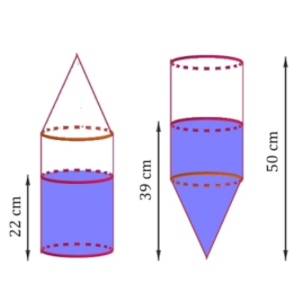
Solución:

Es necesario para hacer este problema conocer las relaciones entre los volúmenes del cono y el cilindro.

La parte ocupada por el líquido del recipiente, cuando está apoyado sobre el cilindro, es un cilindro, por lo que su volumen es el área de la base multiplicada por su altura, que es 22 centímetros (22·a cm³).

Al darle la vuelta, hay un aumento en la altura de 17 centímetros, que equivale al volumen que ocupa un cilindro de 17 centímetros de altura. Eso es lo que hemos perdido en volumen en la parte cónica, que admite un volumen que es la tercera parte de un cilindro de la misma altura.

Si lo tratamos algebraicamente, podemos indicar que 22a = x·a/3 + (39 – x)a, suponiendo que x es la altura del cono. Si dividimos por el área de la base, que es común, y multiplicamos por 3, tendremos que 66 = x + 117 – 3x, por lo que 2x = 51, y por tanto, x = 25,5.

Podemos comprobar que, en efecto, 22 = 25,5/3 + 39 – 25,5.

Así que, de los 50 centímetros, el cono mide 25,5 y el cilindro mide el resto, 24,5. Por lo tanto, su volumen total es de 25,5·a/3 + 24,5·a = 33a, mientras que el volumen ocupado es 22·a, así que la fracción llena sería 22/33 = 2/3. Y ésta es la fracción irreducible que nos piden.