Problema 6 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
En un triángulo ABC, trazamos dos paralelas a la base AB por dos puntos M y N del lado AC, que llegan, respectivamente a los puntos P y R del lado AB.
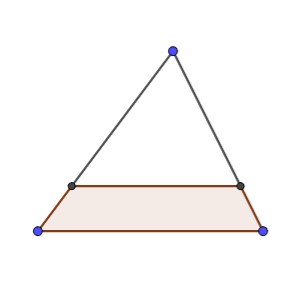
En el primer caso, cuando la trazamos por M, la proporción AM/MC es p y medimos el área del trapecio MABP.
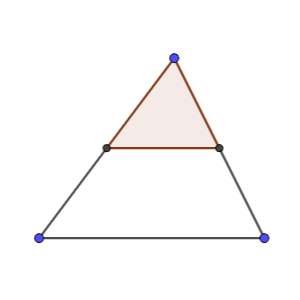
En el segundo caso, medimos el área del triángulo NRC, y resulta ser la misma que la del anterior trapecio. ¿Qué proporción AN/NC hay?
Solución:
Si no tenemos suficiente dominio de la situación, podemos trabajar con un valor concreto de p, por ejemplo 4, y después trasladar a álgebra la situación.
Supongamos que tomamos como área unidad la de todo el triángulo inicial, que es la misma en ambos casos.
El que la proporción AM/MC sea 4, quiere decir que AC/MC = (AM + MC)/MC = 4 + 1 = 5.
Es decir, que el segmento AC es 5 veces mayor que MC. Puesto que los triángulos CMP y CAB son semejantes, es decir, proporcionales, el área de CAB es 1/25 de la original, es decir, la del trapecio es 24/25. Es decir, la proporción entre las áreas del trapecio y de todo el triángulo es de 24/25.
En el segundo dibujo, las figuras CNR y CAB también son semejantes, y la proporción entre esas áreas es de 24/25, luego la proporción entre sus segmentos es de raíz(24)/raíz(25) = 2·raíz(6)/5.
Eso quiere decir que la proporción entre CN/CA es de 2·raíz(6)/5, o CA/CN = 5/(2·raíz(6))
Como nos piden la proporción en AN/NC = (AC – NC)/NC = 5/(2·raíz(6)) – 1 = (5·raíz(6)-12)/12.
Ahora vamos a hacerlo con álgebra:
La proporción AM/MC es p, es decir, AC/MC = (AM + MC)/MC = p + 1.
el área CAB es 1/(p + 1)² de la original.
Por tanto, la del trapecio es la restante, 1 – 1/(p + 1)² = ((p + 1)² – 1)/(p + 1)² = (p² + 2p)/(p +1)². Y también la del triángulo de la segunda figura.
Como en el segundo dibujo, las figuras de nuevo son semejantes, la proporción entre CN/CA será raíz(p² + 2p)/(p + 1). Y la proporción CA/CN = (p+ 1)·raíz(p² + 2p)/(p² + 2p)
Por tanto, la fracción AN/NC = (AC – NC)/NC = (p+ 1)·raíz(p² + 2p)/(p² + 2p) – 1 = ((p+ 1)·raíz(p² + 2p) – p² – 2p)/(p² + 2p).