Problema 7 del concurso Marató de problemes 2024
Se dirige a una edad de: 14-15 años

El numero 8547 tiene la característica de poderse escribir 8547 = 5862 + 2685, como suma de un número abcd de cuatro cifras, y el número de 4 cifras dcba, que resulta de invertir el orden de las cifras del anterior.

Razona cuantos números de 4 cifras tienen la característica de poderse escribir como la suma de un número de 4 cifras abcd y el número dcba que tiene las mismas cifras en orden inverso.

El número más pequeño que cumple el enunciado es el 2002 = 1001 + 1001.

Otro es el 3333, que cumple el enunciado con dos sumas con sumandos diferentes: 3333 = 1122 + 2211 = 1212 + 2121.

¿Cuál es el número más grande que cumple el enunciado? Razona cuántas sumas del tipo abcd + dcba, de dos números de cuatro cifras en el que las cifras de uno resultan de escribir en orden inverso las cifres del otro, dan como resultado este número más grande.

Razona cuántas sumas de dos números de cuatro cifras del tipo abcd + dcba dan como resultado 8547.

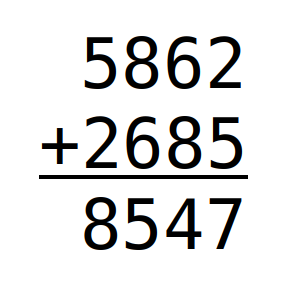
Solución:

Tras tantear un poco, decidí trabajar con la versión algebraica, ya que abcd + dcba = 1000a + 100b + 10c + d + 1000d + 100c + 10b + a = 1001a + 110b + 110c + 1001d = 1001(a + d) + 110(b + c).

Así, los números del tipo que buscamos deben estar compuestos de la suma de un múltiplo de 1001 y de uno de 110, siempre que los factores enteros por los que los multiplicamos estén entre el 2 y el 18 para el 1001 y entre el 0 y el 18 para el 110.

En nuestros ejemplos, 8547 = 7007 + 1540 = 7·1001 + 14·110, 1001 = 1·1001 + 0·110 y 3333 = 3·1001 + 3·110.

Para saber cuántos hay, podemos tratar de ver cuántas combinaciones distintas hay.

El valor (a + d) puede ser 2, y hay 19 combinaciones posibles de valores para el (c + b), ya que la última aún tendría 4 cifras (3982 = 1991 +1991).

Lo mismo sucede si a + d vale 3, 4, 5, 6, 7 y 8 (3995 + 5993 = 9988). Hasta ahora, tenemos 7·19 = 133.

Sin embargo, para el valor de a+d= 9, tenemos que tener cuidado, porque sólo son válidos los números c + b del 0 al 9, porque en ese caso excedemos las 4 cifras (4365 + 5634 = 9999).

Valores mayores de a + d dan más de 4 cifras.

Por tanto en total hay 133 + 10 = 143 números de este tipo. Con más precisión habría que ver que no hemos contado más de una vez cada número, y eso significa que 110k no debe ser múltiplo de 1001. sin embargo, descomponiendo 1001 en factores descubrimos que contiene los factores 13 y 7, mientras que 110 no, es decir, que deberíamos multiplicarlo al menos por 91 para lograrlo.

Evidentemente el número más grande que cumple el enunciado sería el 9999, ya citado anteriormente.

El número 8547 =1001·7 + 110·14. Tenemos que ver cuántos posibles valores a + d suman 7, que serían las parejas 1 y 6, 2 y 5, y 3 y 4, mientras que para conseguir 14 con dos cifras contamos con las opciones 9 y 5, 8 y 6, y 7 y 7. En total, habría por tanto, para cada uno de las tres elecciones de a y de d, 5 elecciones de b y de c (en el caso de que sean 7 ambos no se podrían intercambiar).

Voy a citarlas todas:

1596 + 6951
1686 + 6861
1776 + 6771
1866 + 6681
1956 + 6591
2595 + 5952
2685 + 5862
2775 + 5772
2865 + 5682
2955 + 5592
3594 + 4953
3684 + 4863
3774 + 4773
3864 + 4683
3954 + 4593