Problema 5 del viernes de la Fase Local de la LXI Olimpiada Española de Matemáticas (2025) Se dirige a una edad de: 16-17 años
Sea ABCD un cuadrilátero convexo de forma que AB∩CD = F y AD∩BC = E.
Demuestra que los circuncírculos de los triángulos BFC, AFD, DCE y ABE tienen un punto en común.

Solución:
En un primer momento, debemos dibujar la figura, teniendo en cuenta que los vértices del cuadrilátero están nombrados de forma consecutiva en sentido de las agujas del reloj, o al contrario.
Ningún lado puede ser paralelo al otro, puesto que deben cortarse (la intersección).
Una vez hecho esto, observamos que sucede lo que debemos mostrar, que tienen un punto en común, pero ¿qué tiene de peculiar ese punto?
Para profundizar en esto es conveniente conocer el principio del ángulo central, que nos permite mover un ángulo por un arco de circunferencia, y que en el arco suma 180º con el de su arco opuesto. Esto nos lleva a la situación de que un cuadrilátero está inscrito en una circunferencia sí y sólo si dos de sus ángulos opuestos suman 180º.
Si dibujamos sólo los círculos más pequeños, en este caso, BFC y ABE, está claro que deben cortarse en algún punto, y por tanto este punto pertenece a ambos círculos, y forma dos cuadriláteros que están inscritos cada uno en un círculo. Si llamamos G a este punto, hay muchas coincidencias entre sus ángulos, y vamos a tratar de aprovechar eso.
El ángulo BGC es el mismo que el BEC por pertenecer al círculo común y estar en el mismo arco, y el ángulo EGB es 180º – BAE, por la misma razón, al estar en arcos opuestos.
Pero como la recta AD es la misma que la recta AE, resulta, que el ángulo DAB es el mismo que EGB.
Pero claro, eso quiere decir que BGC y BGE suman lo mismo que DAF (que es igual que DAB) y BFC (que es igual que AFD), y estos ángulos están en el mismo triángulo AFD.
Por tanto, los tres ángulos del triángulo suman 180º, es decir, que el ángulo EDF suma 180º con EGC.
Y eso significa que el cuadrilátero CDEG también está inscrito en una circunferencia, por tanto el punto G pertenece a la circunferencia CDE.
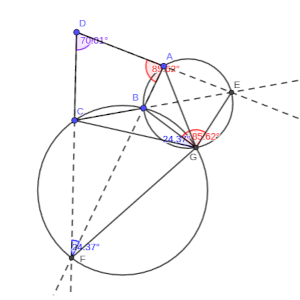
De manera simétrica, podemos razonar que pertenece a la circunferencia DAF, por sumar AGF 180 grados con EDA, al ser suma de los ángulos AGB y FGB.
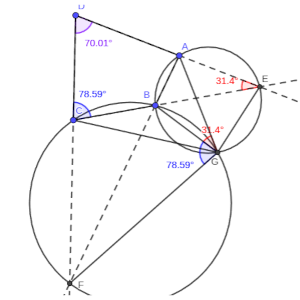
Y, por tanto, el punto G pertenece a los cuatro círculos, como queríamos ver.