Problema 7 de la Fase Local de la Olimpiada Matemática Española (2025)
Se dirige a una edad de: 16-17 años

Halla todos los números enteros a y b que satisfacen la ecuación siguiente:

a(a² + b²) + 7 = 5a² + 3b²

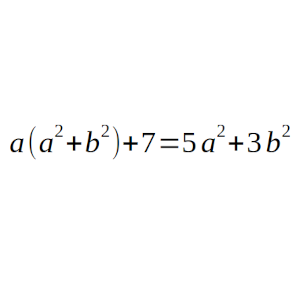
Solución:

Si convertimos la igualdad en un polinomio, tenemos un polinomio de tercer grado en a: a³ – 5a² + ab² + 7 – 3b² = 0.

Puesto que b² es un factor de dos términos, podemos reescribirlo como a³ – 5a² + b²(a – 3) + 7 = 0.

Si a es mayor que 5, los primeros dos sumandos son claramente positivos, y también el tercero, así que no se puede dar la ecuación. Si a es menor que cero, todos los términos son negativos, menos el 7, y claramente el valor absoluto de esos términos es mayor que 7, así que tampoco va a dar cero.

El caso a = 0 se descarta rápidamente, ya que 7 no puede ser 3b².

El resto de casos se pueden ir probando paso a paso, a = 1, a = 2, a = 3, a = 4 y a = 5. Quedan ecuaciones de segundo grado en todos los casos, y las únicas dos soluciones son a = 4, b = 3 y a = 4 y b = -3.