Problema 11 del concurso Marató de problemes 2025 Se dirige a una edad de: 14-15 años
El rectángulo ABCD de la figura está dividido en 6 rectángulos iguales por 5 segmentos paralelos al lado BC.

El punto E del segmento BC tiene la propiedad de que el segmento AE divide al último de los rectángulos pequeños, el que contiene al segmento BC, en dos partes exactamente iguales.
Si suponemos que el triángulo que forma el segmento AE en el primer rectángulo pequeño, el que contiene al segmento AD, tiene un área de 1 cm², calcula el área del rectángulo ABCD.
Solución:
La clave para entender el problema es darse cuenta de que el segmento AE debe pasar por el centro del rectángulo pequeño.
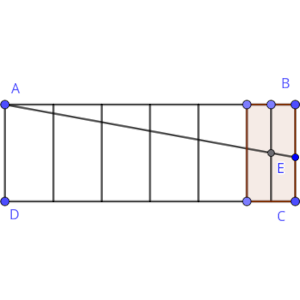
Una vez que esto está claro, dividimos el rectángulo en el doble de rectángulos pequeños, 12, y el punto de corte del segmento último de división (el que sería el decimoprimero) con el segmento AE está en el centro del segmento.
Usando el principio de semejanza, el triángulo que se forma entre el segmento decimoprimero, el segmento AE y el segmento AB guardaría una proporción lineal de escala 5.5 con el triángulo que menciona el problema, por lo que su tamaño sería 5.5 veces más largo y 5.5 veces más alto.
El rectángulo, por tanto, será 6 veces más largo, ya que tiene un segmento más.
El rectángulo será 11 veces más alto, ya que el lado del triángulo de escala 5.5 sobre el segmento decimoprimero lo divide por la mitad.
Como el triángulo tiene la mitad del área de un rectángulo de las mismas dimensiones, un rectángulo que contuviese a ese triángulo tendría un área 2, así que el rectángulo original tendría un área de 2·11·6 = 132 cm².
Otra solución que se me ocurre, más rápida, es pensar que si el triángulo tiene área 1, el siguiente trapecio que forma en el segundo rectángulo tiene área 2 + 1 (el rectángulo que es doble del triángulo original más un tercer triángulo igual), en el tercero tiene área 5, en el cuarto 7, en el quinto 9 y en el sexto 11. Como es la mitad del rectángulo completo, el rectángulo pequeño último mide 22 de área, luego el área de todo el rectángulo grande será 22·6 = 132 cm².