Problema 4 del nivel B de la Fase Comarcal de la de la XXX OMCV 2019
Se dirige a una edad de: 14-15 años

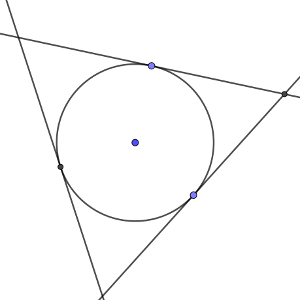
Partimos de un círculo de radio 4 metros.

Desde un punto exterior al círculo, trazamos dos tangentes al mismo, y comprobamos que forman en ese punto un ángulo de 60º.

Si rellenamos de color el área entre las dos tangentes y el círculo ¿qué área queda sombreada?

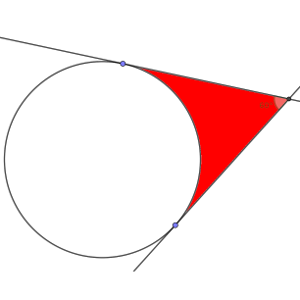
Solución:

Hay varias formas de empezar este problema. La más directa, que prácticamente no necesita usar trigonometría, pasa por trazar los radios del círculo hasta los puntos de tangencia, y unir el centro y el punto exterior.

Así se formarían dos triángulos rectángulos iguales, por simetría. En el punto exterior, entonces, tendrían ángulos de 30º, y por la misma razón formarían un ángulo de 60º en el centro de la circunferencia.

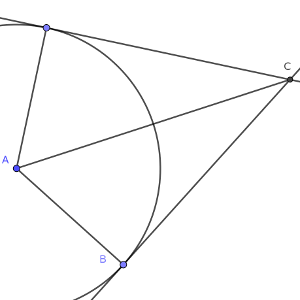
Estos dos triángulos formarían, si los unimos por uno de sus catetos, un triángulo equilátero.

La zona sombreada sería el área de este triángulo menos la zona del círculo que cae en ese ángulo, que es la tercera parte de los 360º del círculo, 120º.

Por tanto, debemos calcular el área del triángulo equilátero (o la suma de los dos rectángulos) y restarle la tercera parte de la circunferencia.

Para el área del triángulo, sabemos que los radios miden 4 metros, y como al unir esos dos triángulos se forma un equilátero, y los radios quedarían como la mitad de un lado, el otro lado, que es la hipotenusa del triángulo original, mide 8 metros.

Para hallar el área, podríamos usar entonces el teorema de Pitágoras y calcular el otro cateto, sabiendo que 64 – 16 = 48, sería la raíz de 48, 6.93. Por lo tanto, el área de cada triángulo rectángulo sería 6.93·4/2, y la suma de ambos valdría 6.93·4 = 27.72. Al restarle la tercera parte del área de la circunferencia, 16·3.14/3 = 16.75, quedaría 10.97 metros. (con más precisión, sería 16·raíz(3) – 16·pi/3 = 16*(raíz(3) – pi/3)).

Hay más alternativas para calcular el área de un triángulo equilátero (8·6.93/2, como base por altura partido por dos, aplicar la fórmula de herón, como raíz de 12·4·4·4, o multiplicar dos lados por el seno del ángulo que forman, 8·8·sen(60)).

Otra manera de abordar le problema sería trazar la linea que une los puntos de tangencia, con lo que tendríamos un triángulo equilátero (sería más difícil conocer su lado, pero una vez que se pudiera hacer, deberíamos restarle al área la de un segmento del círculo, que tampoco sería fácil).

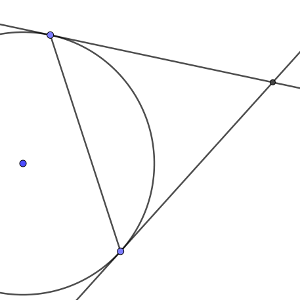
Y una última idea que podría funcionar sería prolongar las líneas de tangencia y construir un triángulo equilátero de forma que el círculo quedara inscrito. El área sería entonces la tercera parte del área del triángulo menos el círculo, aunque tampoco sería algo directo conocer el lado del triángulo.