Problema 3 de nivel A de la Fase Provincial de la de la XXX OMCV 2019
Se dirige a una edad de: 12-13 años

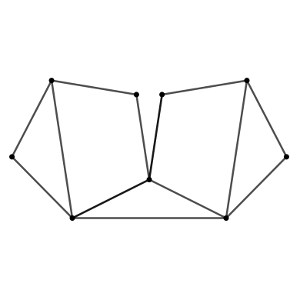
Seguro que conocéis los dibujos que se deben recorrer sin levantar el lápiz del papel ni pasar dos veces por una línea ya trazada.

Para no perdernos, hemos ido numerando los vértices, y hemos obtenido la secuencia 15294758137269.

¿Puedes colocar los números sobre la figura?

Solución:

Para ir directo al grano, sólo hay posibilidad de empezar por dos lugares, y dada la simetría del dibujo, sólo se puede situar el inicio (1) y el final (9) en uno de los dos lugares que tienen tres conexiones, ya que son los únicos con un número impar de caminos que entren o salgan.

Si marcamos los nodos del grafo con letras, como indica el siguiente dibujo, estos lugares son A y E.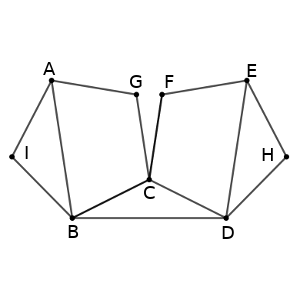

Después, hay unos nodos por los que hay que pasar dos veces (B, C y D, y A y E, claro), y otros por los que sólo hay que pasar una (G, I, F y H).

Viendo las repeticiones que hay en la cadena, se repiten 2, 5 y 7, además del 1 y el 9, así que es fácil identificarlos.

Por tanto, si empezamos por A=1, tenemos que 5 debe ser B, 2 debe ser D, ya que después va al 9, que será E. El siguiente paso, 4, debe ser F, ya que llegamos después a 7, que es el único que se repite que nos falta por visitar, y que debe ser C. Volvemos a 5(B), y vamos a 8, que será I, ya que es de aquellos que sólo se visita una vez. Después vamos a 1(A), 3, que debe ser G, 7(C), 2(D), 6 que sólo puede ser H, y acabamos en 9(E).

Resumiendo, la cadena será 1(A)5(B)2(D)9(E)4(F)7(C)5(B)8(I)1(A)3(G)7(C)2(D)6(H)9(E).

Por supuesto, habría una única otra forma de hacerlo, también valdría una asignación de nombres simétrica, que sería 1(E)5(D)2(B)9(A)4(G)7(C)5(D)8(H)1(E)3(F)7(C)2(B)6(I)9(A).