Problema 3 de la Fase Catalana de la OME 2019 Se dirige a una edad de: 16-17 años
Encontrar los valores del número entero positivo n para los cuales la ecuación xn + (2 + x)n + (2 – x)n = 0 tiene solución entera.
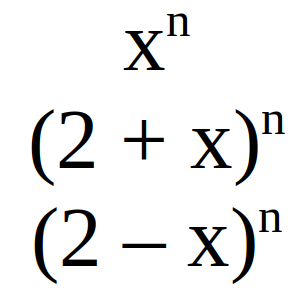
Solución:
Lo primero que debemos hacer es estudiar valores pequeños de n para llegar a alguna conjetura previa.
Para n = 1, tenemos la ecuación x + 2 + x + 2 – x = 0, que evidentemente nos proporciona la solución x = -4, que es entera.
Sin embargo, para n = 2, tenemos la suma de tres números diferentes y positivos, pues son cuadrados, que deben dar 0, por lo que no debe existir ninguna solución real, mucho menos entera. Esto nos ayuda a descartar los valores pares de n en general.
Para n = 3, tenemos un desarrollo que ya nos puede dar alguna idea. Al desarrollar las potencias, tenemos x³ + x³ + 6x² + 12x + 8 + 8 – 12x + 6x² – x³ = 0, es decir, que x³ + 12x² + 16 = 0. Para averiguar si tiene o no solución entera, podemos aplicar el criterio de Ruffini para valores divisores de 16. Además, evidentemente, debemos descartar los valores positivos, en los que no va a dar una solución debido a que todos los sumandos serán positivos.
En general, debemos buscar valores de n impares, y el término independiente que obtendríamos siempre será 2·2n, ya que sumaremos dos veces el sumando 2n. Luego, si existen soluciones enteras, deberán estar en el conjunto de los opuestos de las potencias de 2 hasta 2n + 1.
Además, por el desarrollo del Binomio de Newton, los sumandos de todos los desarrollos son idénticos, excepto en el signo, de forma que los que ocupan una posición impar, que les hace tener un signo negativo en el caso del segundo desarrollo, se anularán, y los otros son todos positivos. Por lo que la suma será un polinomio con todos sus coeficientes positivos. Y eso quiere decir que las únicas potenciales raíces deben ser negativas.
Vamos a cambiar signos en la variable del polinomio para buscar valores positivos en lugar de negativos. De esta forma hay que anular, para valores de n impares y mayores que 1, el polinomio (2 + x)n + (2 – x)n – xn para valores de x potencias de 2.
Evidentemente, para x = 1 no se anula en ningún n (da 3n).
Para x = 2 tampoco, pues da 4n – 2n.
Para otras potencias (t mayor que 1), la expresión queda (2 + 2t)n + (2 – 2t)n – (2t)n = 2n[(1 + 2t – 1)n + (1 – 2t – 1)n – (2t – 1)n]. Puesto que en ese producto el factor 2n no se anula, para dar 0 debe darse que (1 + 2t – 1)n + (1 – 2t – 1)n – (2t – 1)n se anula, pero t es mayor que 1, y n es mayor que 2 (e impar). Todos los sumandos que salgan de ese desarrollo van a tener un factor 4 al menos, excepto los dos 1, que sumarán 2. Eso quiere decir que nunca se van a anular, puesto que sumando múltiplos de cuatro nunca podremos obtener 2 (también podemos razonar módulo 4, es decir, por restos de 4).
Nos recuerda Abel Doñate que este último punto se puede usar (aunque sea un teorema muy reciente, y que requiere una enorme teoría detrás para refrendarlo) el Teorema de Fermat-Wiles (también conocido como último teorema de Fermat), ya que para que esta ecuación tuviera una raíz entera, deberían existir dos enteros elevados a una cierta potencia cuya suma fuera otra potencia del mismo orden, cosa que sabemos que no sucede.