Problema 3 de la Fase Local de la LVI OME 2020
Se dirige a una edad de: 16-17 años

Encuentra todos los posibles valores x, y z, para los que se cumple:
x + y + z = 1
x²y + y²z + z²x = xy² + yz² + zx²
x³ + y² + z = y³ + z² + x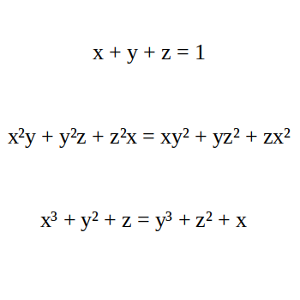
Solución:

Aparentemente, sólo es un sistema de ecuaciones, pero al tener dos de las ecuaciones tercer grado, tanto el método de sustitución como el de reducción no garantizan buenos resultados.

De hecho, aplicar el método de sustitución sólo sería viable si despejamos z, en la primera ecuación (z = 1 – x – y), pero aún así, deberíamos sustituir z², de forma que el aspecto de las dos ecuaciones resultantes asusta un poco. Si lo hacéis, es una vía que tiene futuro, pero es muy difícil. Se debe factorizar los resultados lo más pronto posible, y empezar a solucionar de esa forma.

Otra manera de trabajar sería tratar de factorizar desde el inicio las ecuaciones que tenemos. Para empezar, deberíamos recordar que toda expresión de la forma xⁿ – yⁿ tiene un factor x – y, ya que esta idea aparecerá varias veces en la resolución.

En efecto, sabemos que x² – y² = (x – y)(x + y), pero también es sencillo ver que x³ – y³ = (x – y)(x² + xy + y²), y que x⁴ – y⁴ = (x – y)(x³ + x²y + xy² + y³), aunque sólo es necesario llegar a la segunda igualdad en este caso. La identidad es posible generalizarla usando una especie de suma telescópica.

El caso es que tratamos de factorizar la segunda ecuación por ser la más simétrica. La primera ya es de primer grado y la tercera no es sencilla de factorizar.

Para empezar, interesa igualar a cero (x²y + y²z + z²x – xy² – yz² – zx² = 0). Para tener una pista de si es posible factorizar o no, podemos probar con valores concretos. Pero la estrategia es similar.

Si lo ordenamos como si fuera un polinomio, por ejemplo, en z, escribiríamos z²x – yz²+ y²z – zx² + x²y – xy² = 0, donde observamos que tenemos tres coeficientes, (x – y)z²+ (y² – x²)z + x²y – xy² = 0. Podemos observar que el factor (x – y) aparece en todos los coeficientes, es decir, (x – y)z²+ (y – x)(x + y)z + xy(x – y) = 0. Es decir, que se puede sacar factor común del polinomio (x – y)(z² – (x + y)z + xy). Observa que puesto que y – x = -(x – y), al sacar este último factor aparece un signo en el segundo sumando.

Para encontrar cuáles son las raíces con las que factorizar, podríamos aplicar la fórmula de la ecuación de segundo grado, donde el coeficiente de la z² es ahora 1, el de la z es -(x + y) y el término independiente xy, de forma que los valores de z serían (x + y ± raíz(x² + 2xy + y² – 4xy))/2, pero casualmente el contenido de la raíz se puede simplificar y es un cuadrado perfecto, el de x – y, así que las raíces quedarían (x + y ± raíz(x² – 2xy + y²))/2 = (x + y ± (x – y))/2. Si optamos por la que suma, tenemos que la z vale x y la z que corresponde a la resta es, curiosamente, y.

Así que la factorización es (x – y)(z – x)(z – y) = 0, que nos permite tomar ya una simplificación importante. El producto de tres números reales es cero si y sólo si alguno de los tres lo es, de forma, que en las soluciones, o bien x = y, o bien y = z, o bien x = z. En esos tres supuestos, la ecuación central se cumple (y únicamente en uno de esos casos). Veamos qué significa para las otras dos.

En el caso de que x = y, la primera ecuación será 2x + z = 1, es decir, z = 1 – 2x. En ese caso, la tercera ecuación queda x³ + x² + z = x³ + z² + x, es decir, x² + z = z² + x, y sustituyendo, x² + 1 – 2x = 1 – 4x + 4x² + x, que se transforma en 0 = 3x² – x. Eso proporciona la solución x = 0, y = 0, z = 1, y la solución x = 1/3, y = 1/3, z = 1/3.

En el caso de que x = z, la primera ecuación será 2x + y = 1, es decir, y = 1 – 2x. En ese caso, la tercera ecuación queda x³ + y² + x = y³ + x² + x , es decir, x³ + y² = y³ + x². En este caso, tenemos que x³ – y³ = x² – y², es decir, (x – y)(x² + xy + y²) = (x – y)(x + y). Puesto que el caso en que x = y ya ha sido visto, podemos suponer que x no es igual a y, y dividir por ese factor, con lo que la igualdad queda x² + xy + y² = x + y. Sustituyendo, x² + x – 2x² + 1 – 4x + 4x² = x + 1 – 2x, que se transforma en 3x² – 2x = 0. Eso proporciona la solución x = 0, y = 1, z = 0, y la solución x = 2/3, y = -1/3, z = 2/3.

En el caso de que z = y, la primera ecuación será x + 2y = 1, es decir, x = 1 – 2y. En ese caso, la tercera ecuación queda x³ + y² + y = y³ + y² + x , es decir, x³ + y = y³ + x. En este caso, tenemos que x³ – y³ = x – y, es decir, (x – y)(x² + xy + y²) = x – y. Puesto que el caso en que x = y ya ha sido visto, podemos suponer que x no es igual a y, y dividir por ese factor, con lo que la igualdad queda x² + xy + y² = 1. Sustituyendo, 1 – 4y + 4y² + y – 2y² +y² = 1, que se transforma en 3y² – 3y = 0. Eso proporciona la solución y = 0, x = 1, z = 0, y la solución y = 1, x = -1, z = 1.

Así, las seis únicas soluciones serían (0, 0, 1), (1/3, 1/3, 1/3), (0, 1, 0), (2/3, -1/3, 2/3), (1, 0, 0), y (-1, 1, 1).