Problema 1 de la I Math Home 2020
Se dirige a una edad de: 14-15 años

Dentro de un cuadrado de área 12 se colocan tres triángulos de áreas 4, 5 y 6, respectivamente.

Muestra que dos de los triángulos se solapan en una región de área mayor o igual a 1.

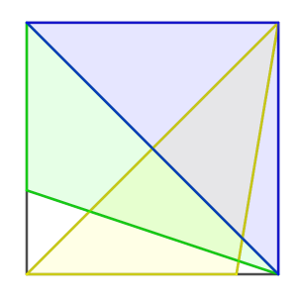
Solución:

En realidad, da igual que las formas que dibujes en el interior del cuadrado tengan formas de triangulo o cualquier otra, así como que el exterior sea un cuadrado o tenga otra forma, siempre que sean medibles.

Cada uno de los puntos del cuadrado cumple que, o bien no está en ninguno de los tres triángulos, o bien sí lo está. Si está dentro del primero, puede ser que esté en otro o no.

Así se llega con paciencia a que el área del cuadrado es igual al área exterior de los tres triángulos más la suma de los tres, menos la suma de las tres intersecciones, más la suma de la intersección de los tres.

Así, Denotando el cuadrado como D y A, B y C los triángulos, a(D) = a(D – A∪B∪C) + a(A) + a(B) + a(C) – a(A∩B) – a(B∩C) – a(A∩C) + a(A∩B∩C).

De esta forma, 12 = a(D – A∪B∪C) + 15 – a(A∩B) – a(B∩C) – a(A∩C) + a(A∩B∩C), por lo que se tiene que a(A∩B) + a(B∩C) + a(A∩C) = 3 + a(D – A∪B∪C) + a(A∩B∩C).

Por lo tanto, si las tres áreas propuestas son menores que 1, alguna de las otras dos debe ser negativa, lo cual es absurdo.