Problema 2 de la Olimpiada Matemática Canadiense de 2008
Se dirige a una edad de: 16-17 años

Encuentra todas las funciones f racionales de variable racional (es decir, del conjunto de los números racionales en sí mismo) que cumplen, para cualquier par de números racionales x e y, la relación f(2f(x) + f(y)) = 2x + y.

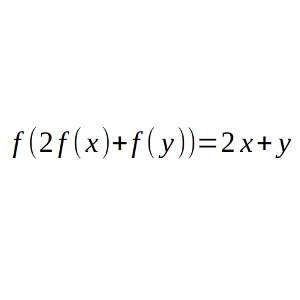
Solución:

Últimamente estoy descubriendo muchos problemas interesantes gracias al canal de youtube de Michael Penn, un profesor americano del Randolph College, de Lynchburg, Virginia. Si dominas el inglés, es una muy buena recomendación.

En este caso, se trata de un problema bastante técnico, en el que se utilizan bastantes de las estrategias habituales a la hora de trabajar con ecuaciones funcionales.

Para empezar, descubrimos algo interesante si tomamos x = y = 0, ya que f(2f(0) + f(0)) = 0, es decir f(3f(0)) = 0.

Pero si ahora, tomamos x = y = 3f(0), entonces la afirmación inicial nos dice que f(2f(3f(0))+f(3f(0)) = 2·3f(0) + 3f(0), pero como sabemos la anterior igualdad, tenemos que f (2·0 + 0) = 6f(0) + 3f(0), por lo que 0 = 8f(0), es decir, f(0) = 0.

Al menos, tenemos ya un valor. Ahora, si tomamos cualquier valor para y, y el valor 0 para x, tenemos que la condición f(2·0 + f(y)) = 2·0 + y, por lo que f(f(y)) = y.

Por lo tanto, f es su propia inversa (y por lo tanto, debe ser biyectiva, es decir, que cada número tiene su imagen diferente, y cada número es imagen de otro).

Entre otras cosas, eso quiere decir que, puesto que f(2f(x) + f(y)) = 2x + y, aplicando f, tenemos que 2f(x) + f(y) = f(2x + y) , que prácticamente es como si fuese lineal.

De hecho, la igualdad anterior, con y = 0, significa que 2f(x) = f(2x), por lo que si tomamos r/2 = x, y cualquier valor para y, la igualdad f(r + y) = f(2x + y) = 2f(x) + f(y) = f(2x) + f(y) = f(r) + f(y), de forma que sí es lineal.

Veamos que en realidad f(x) = f(1)·x.

Resulta que si tenemos un número natural n es fácil probarlo por inducción, ya que si es cierto para n – 1, entonces f(n) = f (1 + n – 1) = f(1) + f(1)(n – 1) = f(1)n. Y, claro, f(1) = f(1)·1.

Y una fracción positiva 1/q lo cumple también, ya que f(1) = f((1/q)·q) = f(1/q + 1/q + … + 1/q) = f(1/q) + f(1/q) + … + f(1/q) = q·f(1/q), luego f(1/q) = f(1)·(1/q).

Evidentemente, entonces, p/q, positiva, también lo cumple, ya que f(p/q) = f(1/q + 1/q + … + 1/q) = f(1/q) + f(1/q) + … + f(1/q) = p·f(1/q) = f(1)·(p/q).

Ahora bien, si tenemos un número racional negativo x, -x es positivo, y como ya hemos visto, f(-x) = f(1)·(-x), y además f(x + (-x)) = f(0) = 0, por lo que f(x) + f(-x) = 0, y eso quiere decir que f(x) = f(1)·x.

Ya casi acabamos, ya que, como sabemos que f(f(1)) = 1, tenemos que f(1)·f(1) = 1, y (f(1))² = 1 sólo puede ocurrir si f(1) = 1 o bien f(1) = -1.

Es decir, que las únicas dos funciones que pueden cumplir la condición inicial serían f(x) = x y la función f(x) = -f(x), y debemos comprobar si las dos cumplen la condición o no.

En efecto, en el primer caso, f(2f(x)+f(y)) = 2f(x) + f(y) = 2x + y. Y en el segundo caso, f(2f(x)+f(y)) = -2f(x) – f(y) = 2x + y.