Problema 10 del concurso marató de problemes 2020
Se dirige a una edad de: 14-15 años

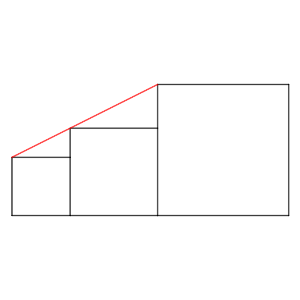
Tres cuadrados que tienen las bases alineadas tienen la propiedad de que su vértice superior izquierdo está alineado.

Suponiendo que tenemos el valor a del lado del cuadrado menor, y el valor b del lado del cuadrado mediano, determina el valor del lado x del lado del cuadrado mayor.

Solución:

Si los tres vértices están alineados, se dará una relación de semejanza entre los dos triángulos que se forman entre los tres cuadrados, como se indica en el dibujo.

Eso significa que (b – a)/a = (x – b)/b.

Puesto que nuestro objetivo es despejar x, debemos eliminar el denominador, de forma que (b² – ab)/a = x – b, de forma que x = (b² – ab)/a + b = b²/a.

Así que el valor de x es b²/a.